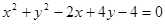题目内容
 定义:平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且单位长度相同)称为平面斜坐标系;在平面斜坐标系xOy中,若
定义:平面内两条相交但不垂直的数轴构成的坐标系(两条数轴的原点重合且单位长度相同)称为平面斜坐标系;在平面斜坐标系xOy中,若| OP |
| e1 |
| e2 |
| e1 |
| e2 |
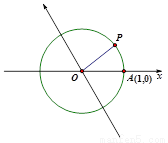
分析:根据斜坐标系的定义,过P作y轴的平行线,交x轴于点B,再利用正弦定理,即可求得点P的坐标.
解答: 解:根据斜坐标系的定义,过P作y轴的平行线,交x轴于点B
解:根据斜坐标系的定义,过P作y轴的平行线,交x轴于点B
在△POB中,∠BOP=θ,∠PBO=60°,|OP|=1,利用正弦定理可得:
=
=
∴|PB|=
sinθ,|OB|=cosθ+
sinθ
∴点P在平面斜坐标系中的坐标是(cosθ+
sinθ,
sinθ)
故选A.
 解:根据斜坐标系的定义,过P作y轴的平行线,交x轴于点B
解:根据斜坐标系的定义,过P作y轴的平行线,交x轴于点B在△POB中,∠BOP=θ,∠PBO=60°,|OP|=1,利用正弦定理可得:
| 1 |
| sin60° |
| |PB| |
| sinθ |
| |OB| |
| sin(θ+60°) |
∴|PB|=
2
| ||
| 3 |
| ||
| 3 |
∴点P在平面斜坐标系中的坐标是(cosθ+
| ||
| 3 |
2
| ||
| 3 |
故选A.
点评:本题考查新定义,考查正弦定理的运用,解题的思路实际上就是仿照平面直角坐标系中点的坐标确定的方法.

练习册系列答案
相关题目
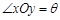 ,平面上任意一点P关于斜坐标系的斜坐标这样定义:若
,平面上任意一点P关于斜坐标系的斜坐标这样定义:若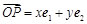 (其中
(其中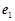 ,
,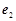 分别是x轴,y轴同方向的单位向量),则P点的斜坐标为(x,y),向量
分别是x轴,y轴同方向的单位向量),则P点的斜坐标为(x,y),向量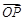 的斜坐标为(x,y).给出以下结论:
的斜坐标为(x,y).给出以下结论: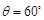 ,P(2,-1),则
,P(2,-1),则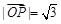 ;
;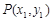 ,
,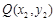 ,则
,则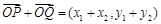 ;
;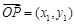 ,
,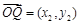 ,则
,则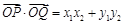 ;
;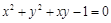 .
.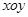 中,若
中,若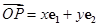 (其中
(其中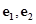 分别是斜坐标系中的
分别是斜坐标系中的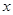 轴和
轴和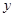 轴正方向上的单位向量,
轴正方向上的单位向量,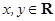 ,
,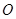 为坐标原点),则称有序数对
为坐标原点),则称有序数对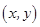 为点
为点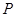 的斜坐标.在平面斜坐标系
的斜坐标.在平面斜坐标系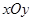 中,若点
中,若点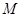 的斜坐标为(1,2),点
的斜坐标为(1,2),点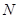 的斜坐标为(3,4),且
的斜坐标为(3,4),且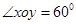 ,则
,则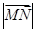 等于 ( )
等于 ( ) 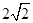 D.
D. 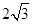
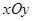 中,若
中,若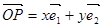 (其中
(其中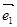 、
、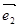 分别是斜坐标系
分别是斜坐标系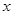 轴、
轴、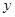 轴正方向上的单位向量,
轴正方向上的单位向量,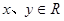 ,
,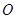 为坐标原点),
为坐标原点), 则有序实数对
则有序实数对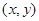 称为点
称为点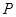 的斜坐标.在平面斜坐标系
的斜坐标.在平面斜坐标系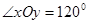 ,点
,点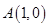 ,
,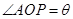 ,点
,点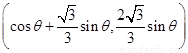 B、
B、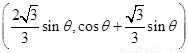
 、
、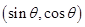 D、
D、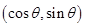
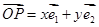 (其中
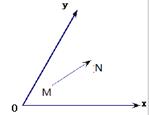
(其中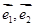 分别是斜坐标系x轴、y轴正方向上的单位向量,x、y∈R,O为坐标系原点),则有序数对(x,y)称为点P的斜坐标.在平面斜坐标系xOy中,若
分别是斜坐标系x轴、y轴正方向上的单位向量,x、y∈R,O为坐标系原点),则有序数对(x,y)称为点P的斜坐标.在平面斜坐标系xOy中,若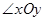 =120°,点M的斜坐标为(1,2),则以点M为圆心,1为半径的圆在斜坐标系xOy中的方程是
( )
=120°,点M的斜坐标为(1,2),则以点M为圆心,1为半径的圆在斜坐标系xOy中的方程是
( )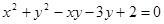 B.
B. 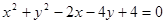
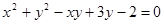 D.
D.