题目内容
直线
（t为参数）与圆
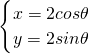（θ为参数）的位置关系是
- A.相离
- B.相切
- C.过圆心
- D.相交不过圆心
A
分析：将直线与圆的参数方程转化为普通方程，利用圆心O（0，0）到直线3x-4y-36=0的距离d=
与该圆的半径2比较即可得到答案．
解答：将直线（t为参数）消掉参数t转化为普通方程为：3x-4y-36=0，
圆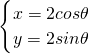（θ为参数）的普通方程为：
=1，即x2+y2=4；
∵圆心O（0，0）到直线3x-4y-36=0的距离d=＞2，
故该直线与圆x2+y2=4相离．
故选A．
点评：本题考查参数方程化成普通方程与直线与圆的位置关系的判断，利用圆心到直线的距离与圆的半径的大小关系是判断的关键，属于基础题．
分析：将直线与圆的参数方程转化为普通方程，利用圆心O（0，0）到直线3x-4y-36=0的距离d=
与该圆的半径2比较即可得到答案．解答：将直线
（t为参数）消掉参数t转化为普通方程为：3x-4y-36=0，圆
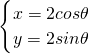（θ为参数）的普通方程为：=1，即x2+y2=4；∵圆心O（0，0）到直线3x-4y-36=0的距离d=
＞2，故该直线与圆x2+y2=4相离．
故选A．
点评：本题考查参数方程化成普通方程与直线与圆的位置关系的判断，利用圆心到直线的距离与圆的半径的大小关系是判断的关键，属于基础题．
练习册系列答案
相关题目
（t为参数）与圆ρ=2cosθ（φ为参数）相切，则此直线的倾斜角α= ．
（t为参数）与圆
（φ为参数）相切，则此直线的倾α= ．
（t为参数）与圆x2+y2-4x=0交于A、B两点，则|PA|•|PB|的值为 ．
（t为参数）与圆
（φ为参数）相切，则此直线的倾α= ．
（t为参数）与圆x2+y2=1有两个交点A，B，若点P的坐标为（2，-1），则|PA|•|PB|= ．