题目内容
12.${∫}_{0}^{1}$(2x+5)(x2+5x-3)10dx等于( )| A. | 0 | B. | $\frac{{3}^{11}}{11}$ | C. | $\frac{2×{3}^{11}}{11}$ | D. | $\frac{{2}^{11}}{11}$ |
分析 根据定积分的计算法则计算即可.
解答 解:${∫}_{0}^{1}$(2x+5)(x2+5x-3)10dx=${∫}_{0}^{1}$(x2+5x-3)10d(2x2+5x+3)=$\frac{1}{11}$(x2+5x-3)11|${\;}_{0}^{1}$=2×$\frac{{3}^{11}}{11}$,
故选:C
点评 本题考查了定积分计算,属于基础题

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
10.为了响应厦门市政府“低碳生活,绿色出行”的号召,思明区委文明办率先全市发起“少开一天车,呵护厦门蓝”绿色出行活动.“从今天开始,从我做起,力争每周至少一天不开车,上下班或公务活动带头选择步行、骑车或乘坐公交车,鼓励拼车…”铿锵有力的话语,传递了绿色出行、低碳生活的理念.
某机构随机调查了本市部分成年市民某月骑车次数,统计如下:
联合国世界卫生组织于2013年确定新的年龄分段:44岁及以下为青年人,45岁至59岁为中年人,60岁及以上为老年人.用样本估计总体的思想,解决如下问题:
(Ⅰ)估计本市一个18岁以上青年人每月骑车的平均次数;
(Ⅱ)若月骑车次数不少于30次者称为“骑行爱好者”,根据这些数据,能否在犯错误的概率不超过0.001的前提下认为“骑行爱好者”与“青年人”有关?
K2=$\frac{n(ad-bc)^{2}}{(a+c)(a+b)(b+d)(c+d)}$.
某机构随机调查了本市部分成年市民某月骑车次数,统计如下:
 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
| 18岁至31岁 | 8 | 12 | 20 | 60 | 140 | 150 |
| 32岁至44岁 | 12 | 28 | 20 | 140 | 60 | 150 |
| 45岁至59岁 | 25 | 50 | 80 | 100 | 225 | 450 |
| 60岁及以上 | 25 | 10 | 10 | 18 | 5 | 2 |
(Ⅰ)估计本市一个18岁以上青年人每月骑车的平均次数;
(Ⅱ)若月骑车次数不少于30次者称为“骑行爱好者”,根据这些数据,能否在犯错误的概率不超过0.001的前提下认为“骑行爱好者”与“青年人”有关?
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
4.一圆的面积以10πcm2/s速度增加,那么当圆半径r=20cm时,其半径r的增加速率u为( )
| A. | $\frac{1}{2}$cm/s | B. | $\frac{1}{3}$cm/s | C. | $\frac{1}{4}$cm/s | D. | $\frac{1}{5}$cm/s |
2.在下列函数中,在定义域上是单调的奇函数的为( )
| A. | y=1 | B. | y=x-1 | C. | y=x+1 | D. | y=x3 |

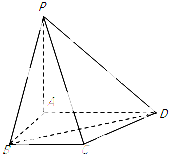 如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2.求二面角A-PD-C的余弦值.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=$\frac{2\sqrt{3}}{3}$,AB=1,BD=PA=2.求二面角A-PD-C的余弦值.