题目内容
10.为了响应厦门市政府“低碳生活,绿色出行”的号召,思明区委文明办率先全市发起“少开一天车,呵护厦门蓝”绿色出行活动.“从今天开始,从我做起,力争每周至少一天不开车,上下班或公务活动带头选择步行、骑车或乘坐公交车,鼓励拼车…”铿锵有力的话语,传递了绿色出行、低碳生活的理念.某机构随机调查了本市部分成年市民某月骑车次数,统计如下:
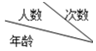 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
| 18岁至31岁 | 8 | 12 | 20 | 60 | 140 | 150 |
| 32岁至44岁 | 12 | 28 | 20 | 140 | 60 | 150 |
| 45岁至59岁 | 25 | 50 | 80 | 100 | 225 | 450 |
| 60岁及以上 | 25 | 10 | 10 | 18 | 5 | 2 |
(Ⅰ)估计本市一个18岁以上青年人每月骑车的平均次数;
(Ⅱ)若月骑车次数不少于30次者称为“骑行爱好者”,根据这些数据,能否在犯错误的概率不超过0.001的前提下认为“骑行爱好者”与“青年人”有关?
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (Ⅰ)利用组中值,即可估计本市一个18岁以上青年人每月骑车的平均次数;
(Ⅱ)根据条件中所给的数据,列出列联表,把求得的数据代入求观测值的公式求出观测值,把观测值同临界值进行比较得到结论.
解答 解:(Ⅰ)估计本市一个18岁以上青年人每月骑车的平均次数为(20×5+40×15+40×25+200×35+200×45+300×55)÷(20+40+40+200+200+300)=42.75;
(Ⅱ)列联表:
| 骑行爱好者 | 非骑行爱好者 | 总计 | |
| 青年人 | 700 | 100 | 800 |
| 非青年人 | 800 | 200 | 1000 |
| 总计 | 1500 | 300 | 1800 |
∴能否在犯错误的概率不超过0.001的前提下认为“骑行爱好者”与“青年人”有关.
点评 本题考查独立性检验的应用,本题解题的关键是根据所给的数据填在列联表中,注意数据的位置不要出错.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.若α,β是两个不同平面,m,n是两条不同直线,则下列结论错误的是( )
| A. | 如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等 | |
| B. | 如果m⊥n,m⊥α,n∥β,那么α⊥β | |
| C. | 如果α∥β,m?α,那么m∥β | |
| D. | 如果m⊥α,n∥α,那么m⊥n |
2.目前,学案导学模式已经成为教学中不可或缺的一部分,为了了解学案的合理使用是否对学生的期末复习有着重要的影响,我校随机抽取100名学生,对学习成绩和学案使用程度进行了调查,统计数据如表所示:
参考公式:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
参考数据:
已知随机抽查这100名学生中的一名学生,抽到善于使用学案的学生概率是0.6.
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法分析:有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
(3)若从学习成绩优秀的同学中随机抽取10人继续调查,采用何种方法较为合理,试说明理由.
| 善于使用学案 | 不善于使用学案 | 总计 | |
| 学习成绩优秀 | 40 | ||
| 学习成绩一般 | 30 | ||
| 总计 | 100 |
参考数据:
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法分析:有多大的把握认为学生的学习成绩与对待学案的使用态度有关?
(3)若从学习成绩优秀的同学中随机抽取10人继续调查,采用何种方法较为合理,试说明理由.
12.${∫}_{0}^{1}$(2x+5)(x2+5x-3)10dx等于( )
| A. | 0 | B. | $\frac{{3}^{11}}{11}$ | C. | $\frac{2×{3}^{11}}{11}$ | D. | $\frac{{2}^{11}}{11}$ |
 将石子摆成如图所示的梯形形状,称数列5,9,14,20,…为“梯形数”.根据图形的构成,此数列的第100项,即a100=5252.
将石子摆成如图所示的梯形形状,称数列5,9,14,20,…为“梯形数”.根据图形的构成,此数列的第100项,即a100=5252.