题目内容
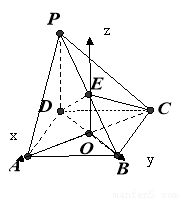
(本小题满分12分)如图,在四棱锥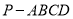 中,
中,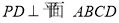 ,四边形
,四边形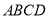 是菱形,
是菱形,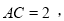
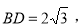 且
且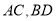 交于点
交于点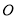 ,
,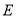 是
是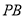 上任意一点.
上任意一点.

(1)求证: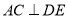 ;
;
(2)已知二面角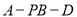 的余弦值为
的余弦值为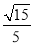 ,若
,若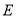 为
为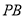 的中点,求
的中点,求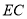 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(1)证明见解析;(2)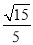 .
.
【解析】
试题分析:(1)线线垂直问题转化为线面问题即可解决,即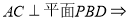
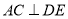 ,由
,由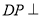 平面
平面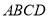 ,得
,得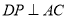 ,又分析可知
,又分析可知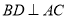 ,且
,且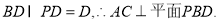 ,所以
,所以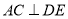 (2)解法1:(空间向量在立体几何中的应用)设
(2)解法1:(空间向量在立体几何中的应用)设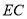 与平面
与平面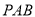 所成的角为
所成的角为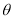 ,即
,即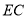 与平面
与平面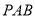 所成角为
所成角为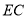 与平面
与平面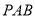 的法向量
的法向量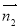 所成角,如图所示的空间直角坐标系,
所成角,如图所示的空间直角坐标系,
设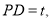 则
则 ,
,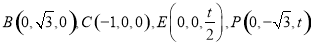 ,
,
平面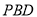 的一个法向量为
的一个法向量为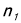 (1,0,0),
(1,0,0),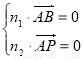 ,得到
,得到
再由二面角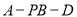 的余弦值为
的余弦值为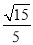 ,
, ,解得
,解得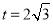 ,
,
故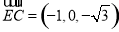 ,
,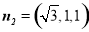 ,最后
,最后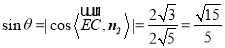 求得;
求得;
解法2:通过构造法作出二面角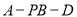 的平面角
的平面角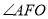 ,
,
设DP=t, 作出二面角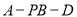 的平面角
的平面角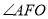 ,
,
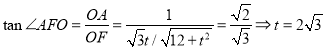
由 ,求出点
,求出点 到平面
到平面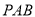 的距离
的距离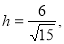
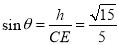
试题解析:(1)因为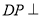 平面
平面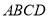 ,所以
,所以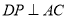 , 1分
, 1分
因为四边形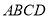 为菱形,所以
为菱形,所以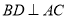 2分
2分
又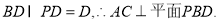
因为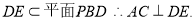 5分
5分
(2)解法1:
连接 在
在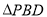 中,
中,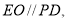
所以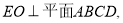 分别以
分别以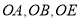 所在直线为
所在直线为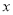 轴,
轴,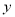 轴,
轴, 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
设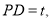 则
则 ,
,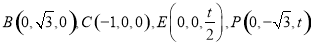 . 6分
. 6分
由(1)知,平面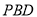 的一个法向量为
的一个法向量为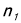 (1,0,0), 设平面
(1,0,0), 设平面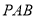 的一个法向量为
的一个法向量为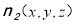 ,则
,则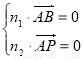 得
得 ,令
,令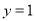 ,得
,得 8分
8分
因为二面角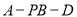 的余弦值为
的余弦值为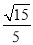 ,所以
,所以 ,
,
解得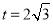 或
或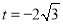 (舍去),所以
(舍去),所以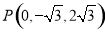 10分
10分
设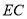 与平面
与平面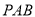 所成的角为
所成的角为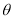 .因为
.因为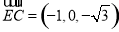 ,
,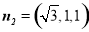 ,
,
∴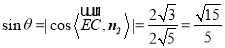
所以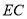 与平面
与平面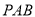 所成角的正弦值为
所成角的正弦值为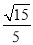 . 12分
. 12分
解法2:
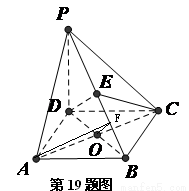
设DP=t, 作出二面角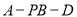 的平面角
的平面角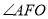
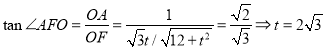
 由
由 ,求出点
,求出点 到平面
到平面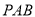 的距离
的距离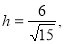
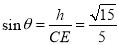 .
.
考点:1、线面垂直和线线垂直的互化;2、空间向量在立体几何中的应用;3、空间想象能力和综合分析能力.

练习册系列答案
相关题目
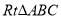 (
(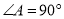 )的外接圆为圆
)的外接圆为圆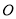 ,过
,过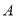 的切线
的切线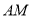 交
交 于点
于点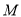 ,过
,过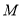 作直线交
作直线交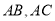 于点
于点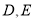 ,且
,且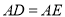

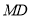 平分角
平分角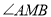 ;
;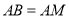 ,求
,求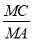 的值.
的值. ,
, ,则
,则 的值为( )
的值为( ) B.
B. C.
C. D.
D.
 若关于x的方程
若关于x的方程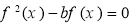 恰有三个不同的实数解,则实数b的取值范围是( ).
恰有三个不同的实数解,则实数b的取值范围是( ). 的定义域是( ).
的定义域是( ). B.
B. C.
C. D.
D.
 满足
满足 ,向量
,向量 .若
.若 ,则实数m的最小值为 .
,则实数m的最小值为 .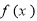 在区间
在区间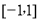 上的解析式是
上的解析式是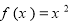 ,则函数
,则函数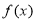 在实数集R上的图象与函数
在实数集R上的图象与函数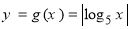 的图象的交点的个数是 ( ).
的图象的交点的个数是 ( ).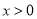 ,则“
,则“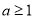 ”是“
”是“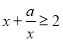 恒成立”的( )
恒成立”的( )
 B.
B.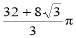
 D.
D.