题目内容
利用单调性定义证明:函数f(x)=
解析:本题是利用单调性定义证明单调性的一个典型例子,由于函数的定义域没有给出,证明前要先求出定义域,然后证明.
证明:证法一:函数f(x)=![]() 的定义域是x∈[1,+∞),任取x1、x2∈[1,+∞)且x1<x2,
的定义域是x∈[1,+∞),任取x1、x2∈[1,+∞)且x1<x2,
则f(x2)-f(x1)=![]() -
-![]()
=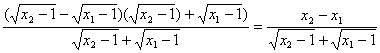 .
.
∵x1、x2∈[1,+∞),且x1<x2,∴![]() +
+![]() >0,x2-x1>0.
>0,x2-x1>0.
∴f(x1)<f(x2),即函数f(x)=![]() 在定义域上是增函数.
在定义域上是增函数.
证法二:函数f(x)=![]() 的定义域是x∈[1,+∞],任取x1、x2∈[1,+∞)且x1<x2,
的定义域是x∈[1,+∞],任取x1、x2∈[1,+∞)且x1<x2,
则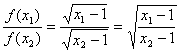 ,
,
∵x1、x2∈[1,+∞),且x1<x2,∴0≤x1-1<x2-1.
∴0≤![]() <1.∴
<1.∴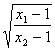 <1.∵f(x2)=
<1.∵f(x2)=![]() >0,∴f(x1)<f(x2).
>0,∴f(x1)<f(x2).
∴函数f(x)=![]() 在定义域[1,+∞)上是增函数.
在定义域[1,+∞)上是增函数.

练习册系列答案
相关题目
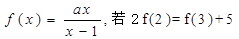 ,
,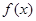 在区间
在区间 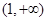 的单调性.
的单调性.