题目内容
利用单调性定义证明函数f(x)=x+
在[1,2]上的单调性并求其最值.
| 4 | x |
分析:利用函数单调性的定义,设1≤x1<x2≤2,利用作差法比较f(x1)与f(x2)的大小,进而证明函数f(x)为单调减函数,再利用单调性求函数最值即可
解答:解:设1≤x1<x2≤2,
则f(x1)-f(x2)=x1+
-x2-
=x1-x2+
∵
,∴
,x1x2>0
∴f(x1)>f(x2)
∴函数f(x)=x+
在[1,2]上为减函数
∴当x=2时,f(x)取得最小值4,当x=1时,f(x)取得最大值5.
则f(x1)-f(x2)=x1+
| 4 |
| x1 |
| 4 |
| x2 |
| 4(x2-x1) |
| x1x2 |
|
∵
|
|
∴f(x1)>f(x2)
∴函数f(x)=x+
| 4 |
| x |
∴当x=2时,f(x)取得最小值4,当x=1时,f(x)取得最大值5.
点评:本题主要考查了函数单调性的定义,利用定义证明函数的单调性的方法和步骤,作差法比较大小,代数变形能力,属基础题

练习册系列答案
相关题目
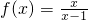 ,x∈[2,4]是单调递减函数,并求函数的值域.
,x∈[2,4]是单调递减函数,并求函数的值域. ,x∈[2,4]是单调递减函数,并求函数的值域.
,x∈[2,4]是单调递减函数,并求函数的值域.