题目内容
11.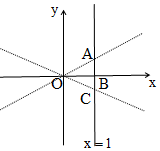 已知双曲线C:$\frac{x^2}{3}-\frac{y^2}{b^2}$=1(b>0)的右焦点为(2,0).
已知双曲线C:$\frac{x^2}{3}-\frac{y^2}{b^2}$=1(b>0)的右焦点为(2,0).(1)求双曲线C的渐近线方程.
(2)双曲线C的两条渐近线与直线x=1所围成的三角形面积.
分析 (1)由题意可得c=2,结合a,b,c的关系,可得b=1,进而得到双曲线的渐近线方程;
(2)求得渐近线与直线x=1的交点,可得交点间的距离,运用三角形的面积公式计算即可得到所求.
解答 解:(1)双曲线C:$\frac{x^2}{3}-\frac{y^2}{b^2}$=1的右焦点为(2,0),
可得3+b2=c2=4,解得b=1,
可得双曲线的渐近线方程为y=±$\frac{\sqrt{3}}{3}$x;
(2)双曲线C的两条渐近线与直线x=1的交点为(1,$\frac{\sqrt{3}}{3}$),(1,-$\frac{\sqrt{3}}{3}$),
可得所围成的三角形面积为$\frac{1}{2}$×1×$\frac{2\sqrt{3}}{3}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查了双曲线的方程和性质,主要是渐近线方程及运用,考查三角形的面积的计算,考查了运算能力,属于基础题.

练习册系列答案
相关题目
18.《九章算术》有这样一个问题:今有女子善织,日增等尺,第二日、第五日、第八日所织之和为十五尺,九日共织尺数是( )
| A. | 5 | B. | 15 | C. | 45 | D. | 10 |
6.已知集合A={x|x2-3x+2=0},集合B={x|logx4=2},则A∪B=( )
| A. | {-2,1,2} | B. | {-2,2} | C. | {1,2} | D. | {2} |
16.若集合M={1,2},N={2,3},则集合M∪N真子集的个数是.( )
| A. | 7 | B. | 8 | C. | 15 | D. | 16 |
3.若f′(x0)=-3,则$\underset{lim}{h→0}$$\frac{f({x}_{0}+h)-f({x}_{0}-3h)}{h}$=( )
| A. | -10 | B. | -11 | C. | -12 | D. | -16 |
20.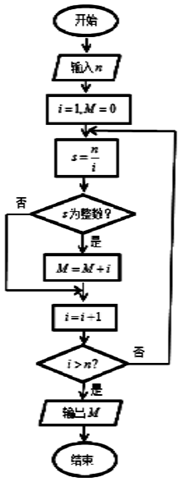 执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )
执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )
 执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )
执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )| A. | 66 | B. | 65 | C. | 64 | D. | 63 |