题目内容
7.已知a,b∈(0,e),且a<b,则下列式子中正确的是( )| A. | alnb<blna | B. | alnb>blna | C. | alna>blnb | D. | alna<blnb |
分析 先构造函数$f(x)=\frac{lnx}{x}$,利用导数判断函数在(0,e)上的单调性,即可得到alnb>blna,再构造函数g(x)=xlnx,判断函数的单调性,即可解决.
解答 解:设$f(x)=\frac{lnx}{x}$,则$f'(x)=\frac{1-lnx}{x^2}$,
在(0,e)上,f'(x)>0,f(x)单调递增,
所以f(a)<f(b),即$\frac{lna}{a}<\frac{lnb}{b},blna<alnb$;
设g(x)=xlnx,则g'(x)=1+lnx,
当$x∈(0,\frac{1}{e})$时,g'(x)<0,g(x)单调递减,
当$x∈(\frac{1}{e},e)$时,g'(x)>0,g(x)单调递增,
∴C,D均不正确,
故选:B
点评 本题考查了导数和函数的单调性的关系,以及导数的应用,属于中档题.

练习册系列答案
相关题目
17.如图所示是正三棱锥V-ABC的正视图,侧视图和俯视图,则其正视图的面积为( ) 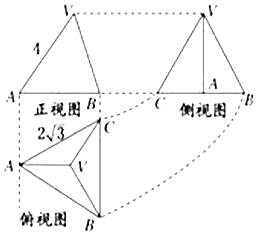

| A. | 6 | B. | 5 | C. | 4$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
2.函数y=lnx-x在x∈(0,e]上的最大值为( )
| A. | e | B. | 1 | C. | -e | D. | -1 |
12.当点P在圆x2+y2=1上变动时,它与定点Q(3,0)相连,线段PQ的中点M的轨迹方程是( )
| A. | (x-3)2+y2=1 | B. | (2x-3)2+4y2=1 | C. | (x+3)2+y2=4 | D. | (2x+3)2+4y2=4 |
17.已知命题p:?x∈R,2x>0,那么命题¬p为( )
| A. | ?x∈R,2x<0 | B. | ?x∈R,2x<0 | C. | ?x∈R,2x≤0 | D. | ?x∈R,2x≤0 |