Question

1．已知函数f（x）=$\sqrt{{x}^{2}-6x+9}$+$\sqrt{{x}^{2}+2x+1}$
（1）作出y=f（x）的图象；
（2）解不等式f（x）≤6；
（3）设函数g（x）=k（x-3），k∈R，若f（x）＞g（x）对任意的x∈R都成立，求k的取值范围．

Answer 1

分析 （1）函数f（x）=|x-3|+|x+1|，通过零点分区间法，可得分段函数f（x）的解析式，画出图象；
（2）不等式f（x）≤6即|x-3|+|x+1|≤6．可得$\left\{\begin{array}{l}{2-2x≤6}\\{x≤-1}\end{array}\right.$或$\left\{\begin{array}{l}{4≤6}\\{-1＜x＜3}\end{array}\right.$或$\left\{\begin{array}{l}{2x-2≤6}\\{x≥3}\end{array}\right.$，分别求得它们的解集，再取并集，即得所求；
（3）由题意可得，f（x）的图象恒在g（x）图象的上方，作函数y=f（x）和 y=g（x）的图象如图，由k_PB=2，A（-1，4），可得k_PA=-1，数形结合求得实数k的取值范围．

解答 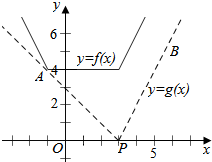解：（1）函数f（x）=|x-3|+|x+1|
=$\left\{\begin{array}{l}{2-2x，x≤-1}\\{4，-1＜x＜3}\\{2x-2，x≥3}\end{array}\right.$，如图所示．
（2）f（x）≤6即为
$\left\{\begin{array}{l}{2-2x≤6}\\{x≤-1}\end{array}\right.$或$\left\{\begin{array}{l}{4≤6}\\{-1＜x＜3}\end{array}\right.$或$\left\{\begin{array}{l}{2x-2≤6}\\{x≥3}\end{array}\right.$，
可得-2≤x≤-1或-1＜x＜3或3≤x≤4．
所以f（x）≤6的解集为{x|-2≤x≤4}．
（3）f（x）＞g（x）对任意的x∈R都成立，
即f（x）的图象恒在g（x）图象的上方，
∵f（x）=|x-3|+|x+1|=$\left\{\begin{array}{l}{2-2x，x≤-1}\\{4，-1＜x＜3}\\{2x-2，x≥3}\end{array}\right.$．
由于函数g（x）=k（x-3）的图象为恒过定点P（3，0），且斜率k变化的一条直线，
作函数y=f（x）和 y=g（x）的图象如图，其中，k_PB=2，A（-1，4），
∴k_PA=$\frac{4-0}{-1-3}$=-1．
由图可知，要使得f（x）的图象恒在g（x）图象的上方，
∴实数k的取值范围为（-1，2]．

点评 本题主要考查含绝对值的函数的图象和应用，绝对值不等式的解法，体现了转化、分类讨论、数形结合的数学思想，属于中档题．