Question

1．已知函数f（x）=x²-4a²lnx，若方程f（x）=2ax有唯一正实根，则实数a=$\frac{1}{2}$．

Answer 1

分析 方程f（x）=2ax有唯一正实根，即为x²-2ax=4a²lnx即有（x-a）²=a²（4lnx+1），作出函数y=（x-a）²和y=a²（4lnx+1）的图象，发现可得它们相切时，有一个公共点，此时a＞0，设出切点（m，n），运用切线的斜率相等，点满足曲线方程，解方程可得a．

解答 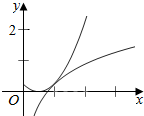解：方程f（x）=2ax有唯一正实根，即为
x²-2ax=4a²lnx即有（x-a）²=a²（4lnx+1），
作出函数y=（x-a）²和y=a²（4lnx+1）的图象，
发现可得它们相切时，有一个公共点，此时a＞0，
即方程有唯一正实根．
设出切点为（m，n），由y=（x-a）²的导数为y′=2（x-a），
y=a²（4lnx+1）的导数为y′=$\frac{4{a}^{2}}{x}$，
即有2（m-a）=$\frac{4{a}^{2}}{m}$，可得m=2a，
又（m-a）²=a²（4lnm+1），即有lnm=0，
解得m=1，a=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．

点评 本题考查函数方程的转化思想，考查数形结合的思想方法，以及运算能力，属于中档题．