题目内容
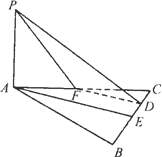
如图,已知在边长为![]() 的正三角形ABC中,E、F分别为BC和AC的中点,PA⊥面ABC,且PA=2,设平面α过PF且与AE平行.求AE与平面α间的距离.
的正三角形ABC中,E、F分别为BC和AC的中点,PA⊥面ABC,且PA=2,设平面α过PF且与AE平行.求AE与平面α间的距离.
答案:
解析:
解析:
|
解:设α∩平面ABC=FD,D∈BC,∵AE∥α,∴AE∥FD, ∵F为AC的中点,∴D为EC中点, 在平面ABC内,过A作AG⊥DF的延长线于G,联结PG, ∵PA⊥平面ABC,∴PG⊥DF, ∵AG∩PG于G,∴DG⊥平面PAG, 而 过A作AH⊥PG于H,则AH⊥α, ∴AH的长为A到平面α的距离,也即直线AE到α的距离, ∵AE∥FD,AE⊥BC,∴FD⊥BC, 又AG∥DE,∴ ∴ 即所求的距离为 |

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
 ,
, 如图游泳者站在边长为100米的正方形游泳池ABCD中A处,希望从A步行到E处(E为边AB上的点),再从E游到C,已知此人步行的速度为v1米/秒,游泳的速度为
如图游泳者站在边长为100米的正方形游泳池ABCD中A处,希望从A步行到E处(E为边AB上的点),再从E游到C,已知此人步行的速度为v1米/秒,游泳的速度为 的左、右焦点为
的左、右焦点为 ,其上顶点为
,其上顶点为 .已知
.已知 是边长为
是边长为 的正三角形.
的正三角形. 任作一动直线
任作一动直线 交椭圆C于
交椭圆C于 两点,记
两点,记 若在线段
若在线段 上取一点
上取一点 使得
使得 ,试判断当直线
,试判断当直线 是否在某一定直线上运动?若在,请求出该定直线的方程;若不在,请说明理由.
是否在某一定直线上运动?若在,请求出该定直线的方程;若不在,请说明理由.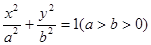 的左、右焦点为
的左、右焦点为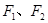 ,其上顶点为
,其上顶点为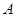 .已知
.已知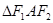 是边长为
是边长为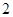 的正三角形.
的正三角形.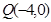 任作一直线
任作一直线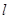 交椭圆C于
交椭圆C于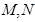 两点,记
两点,记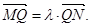 若在线段
若在线段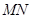 上取一点
上取一点 使得
使得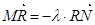 ,试判断当直线
,试判断当直线 是否在某一定直线上运动?若在,请求出该定直线的方程,若不在,请说明理由.
是否在某一定直线上运动?若在,请求出该定直线的方程,若不在,请说明理由.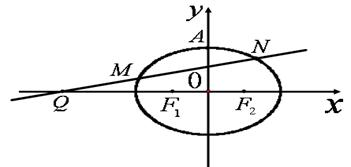
 的正方形
的正方形
 为圆心作半径为
为圆心作半径为 的圆弧与正方形交于
的圆弧与正方形交于 、
、 两点,在
两点,在 上有一动点
上有一动点 ,过
,过 ,求矩形
,求矩形 面积的最小值;
面积的最小值; 。
。