题目内容
 如图游泳者站在边长为100米的正方形游泳池ABCD中A处,希望从A步行到E处(E为边AB上的点),再从E游到C,已知此人步行的速度为v1米/秒,游泳的速度为
如图游泳者站在边长为100米的正方形游泳池ABCD中A处,希望从A步行到E处(E为边AB上的点),再从E游到C,已知此人步行的速度为v1米/秒,游泳的速度为| v1 | 2 |
(1)设∠BCE=θ,试将此人按上述路线从A到C所需时间t秒表示为θ的函数.
(2)θ为何值时,此人从A经E到C所需时间t最小,其最小值是多少?
分析:(1)在Rt△CBE中,分别表示出BE,CE,AE的表达式,进而分别根据步行的速度和游泳的速度分别表示从A到E和从E到C得时间,求得从A到C所需时间t秒表示为θ的函数.
(2)令y=
-tanθ,设出P的坐标,进而可推断出
表示P与点A(0,2)连线的斜率,进而可知当直线与圆相切时,斜率最大,进而求得此时θ的值.
(2)令y=
| 2 |
| cosθ |
| sinθ-2 |
| cosθ |
解答: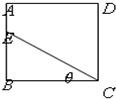 解:(1)在Rt△CBE中,BE=100tanθ,CE=
解:(1)在Rt△CBE中,BE=100tanθ,CE=
AE=100-100tanθ
所以T=
+
.
=
+
(
-tanθ),0≤θ≤
(2)令y=
-tanθ,则y=-
设P(cosθ,sinθ),则P在单位圆第一象限的八分一圆上,
表示P与点A(0,2)连线的斜率,
当直线与圆相切时,斜率最大,
此时∠OAP=
,
的最大值是
-tan60°=-
,即最大值时即要θ=
所以所求的ymin=
.
 解:(1)在Rt△CBE中,BE=100tanθ,CE=
解:(1)在Rt△CBE中,BE=100tanθ,CE=| 100 |
| COSθ |
AE=100-100tanθ
所以T=
| 100-100tanθ |
| v1 |
| ||
|
=
| 100 |
| v1 |
| 100 |
| v1 |
| 2 |
| cosθ |
| π |
| 4 |
(2)令y=
| 2 |
| cosθ |
| sinθ-2 |
| cosθ |
设P(cosθ,sinθ),则P在单位圆第一象限的八分一圆上,
| sinθ-2 |
| cosθ |
当直线与圆相切时,斜率最大,
此时∠OAP=
| π |
| 6 |
| sinθ-2 |
| cosθ |
-tan60°=-
| 3 |
| π |
| 6 |
所以所求的ymin=
100(1+
| ||
| v1 |
点评:本题主要考查了解三角形的实际应用.考查了学生分析问题和解决实际问题的能力以及数形结合的思想的运用.

练习册系列答案
相关题目



 .米/秒.
.米/秒.