题目内容
若函数f（x）=mx2+（m-1）x+m有零点，则实数m的取值范围
[-1，
]
| 1 |
| 3 |
[-1，
]
．| 1 |
| 3 |
分析：利用函数零点的存在定理解决本题，要对该函数的性质进行讨论，是否为二次函数，是否有等根等．注意分类讨论思想的运用．
解答：解：①若m=0，则f（x）=-x，
它的零点为0∉，
故m=0符合题意，
②若m≠0，
函数f（x）=mx2+（m-1）x+m有零点，
必有△=（m-1）2-4m2≥0⇒-1≤m≤
，且m≠0，
综上实数m的取值范围为：[-1，
]
故答案为：[-1，
]．
它的零点为0∉，
故m=0符合题意，
②若m≠0，
函数f（x）=mx2+（m-1）x+m有零点，
必有△=（m-1）2-4m2≥0⇒-1≤m≤
| 1 |
| 3 |
综上实数m的取值范围为：[-1，
| 1 |
| 3 |
故答案为：[-1，
| 1 |
| 3 |
点评：本题考查函数零点的确定，考查函数在某个区间内有零点的转化方法，注意对二次项系数的讨论．考查学生的分类讨论思想，属中档题．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
和圆x2+y2=n2相切，其中m，n∈N，0＜|m-n|≤1，若函数f（x）=mx+1-n的零点x∈（k，k+1）k∈Z，则k= ．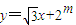
和圆x2+y2=n2相切，其中m，n∈N，0＜|m-n|≤1，若函数f（x）=mx+1-n的零点x∈（k，k+1）k∈Z，则k= ．