题目内容
8.设a=2-2,$b={3^{\frac{1}{2}}}$,c=log25,则a,b,c的大小关系为( )| A. | a<c<b | B. | b<a<c | C. | b<c<a | D. | a<b<c |
分析 利用指数函数、对数函数的单调性求解.
解答 解:∵a=2-2=$\frac{1}{4}$,1=30<$b={3^{\frac{1}{2}}}$=$\sqrt{3}$<2,
c=log25>log24=2,
∴a<b<c.
故选:D.
点评 本题考查三个数的大小的比较,是基础题,解题时要认真审题,注意利用指数函数、对数函数的单调性的合理运用.

练习册系列答案
相关题目
18.已知函数f(x)=|lnx|-1,g(x)=-x2+2x+3,用min{m,n}表示m,n中的最小值,设函数h(x)=min{f(x),g(x)},则函数h(x)的零点个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
19.已知集合M满足{1,2}⊆M?{1,2,3,4},则集合M的个数是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
20.函数y=x+$\frac{1}{x-1}$+1(x>1)的最小值是( )
| A. | -2 | B. | 2 | C. | -4 | D. | 4 |
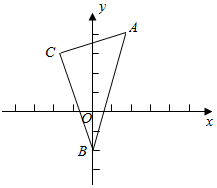 如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3),求:
如图,已知三角形的顶点为A(2,4),B(0,-2),C(-2,3),求: