题目内容
15．函数f（x）=$\left\{\begin{array}{l}{{e}^{x}，x≥0}\\{-2x，x＜0}\end{array}\right.$，若关于x的方程f[f（x）]+k=0恰有两个不等实数根x1，x2，则x1+x2的最大值为（ ）| A． | -$\frac{1}{2}+ln2$ | B． | $\frac{1}{2}-ln2$ | C． | -1+ln2 | D． | 1+ln2 |
分析 可判断f（x）＞0恒成立；从而化简方程为f（x）=ln（-k）；从而作图辅助，可知存在实数a（a≥1），使-2x1=a=e${\;}^{{x}_{2}}$，从而可得x1+x2=-$\frac{a}{2}$+lna，再构造函数g（a）=-$\frac{a}{2}$+lna，求导g′（a）=-$\frac{1}{2}$+$\frac{1}{a}$=$\frac{2-a}{2a}$，从而确定最值．
解答 解：∵f（x）=$\left\{\begin{array}{l}{{e}^{x}，x≥0}\\{-2x，x＜0}\end{array}\right.$，∴f（x）＞0恒成立；
∴f[f（x）]=ef（x），
∵f[f（x）]+k=0，
∴ef（x）+k=0，即f（x）=ln（-k）；
作函数f（x）=$\left\{\begin{array}{l}{{e}^{x}，x≥0}\\{-2x，x＜0}\end{array}\right.$与y=ln（-k）的图象如下，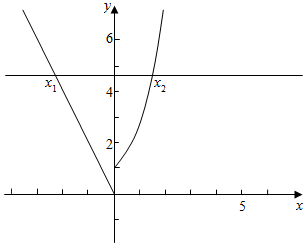
，
结合图象可知，存在实数a（a≥1），使-2x1=a=e${\;}^{{x}_{2}}$，
故x1+x2=-$\frac{a}{2}$+lna，
令g（a）=-$\frac{a}{2}$+lna，则g′（a）=-$\frac{1}{2}$+$\frac{1}{a}$=$\frac{2-a}{2a}$，
故当a=2时，x1+x2有最大值-1+ln2；
故选C．
点评 本题考查了复合函数与分段函数的应用，同时考查了导数的综合应用及最值问题，应用了数形结合的思想及转化构造的方法．
练习册系列答案
阅读快车系列答案
相关题目
13．将函数f（x）=2sin（3x+φ）（-π＜φ＜π）的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变）得到函数g（x）的图象，且对任意的x∈R有g（x）+g（$\frac{π}{4}$）≥0，则g（x）的单调递增区间为（ ）
| A． | [$\frac{kπ}{3}$+$\frac{π}{4}$，$\frac{kπ}{3}$+$\frac{5π}{12}$]，k∈Z | B． | [$\frac{kπ}{3}$+$\frac{π}{12}$，$\frac{kπ}{3}$+$\frac{π}{4}$]，k∈Z | ||
| C． | [$\frac{4kπ}{3}$+$\frac{π}{4}$，$\frac{4kπ}{3}$+$\frac{11π}{12}$]，k∈Z | D． | [$\frac{4kπ}{3}$-$\frac{5π}{12}$，$\frac{4kπ}{3}$+$\frac{π}{4}$]，k∈Z |
△ABC中，AB=1，AC=2．
7．已知函数$f（x）=\left\{{\begin{array}{l}{x+\frac{1}{2}，x∈[0，\frac{1}{2}）}\\{{2^{x-1}}，x∈[\frac{1}{2}，2）}\end{array}}\right.$，若存在x1，x2，当0≤x1＜x2＜2时，f（x1）=f（x2），则x1f（x2）-f（x2）的取值范围为（ ）
| A． | $（0，\frac{{2-3\sqrt{2}}}{4}）$ | B． | $[-\frac{9}{16}，\frac{{2-3\sqrt{2}}}{4}）$ | C． | $[\frac{{2-3\sqrt{2}}}{4}，-\frac{1}{2}）$ | D． | $[-\frac{9}{16}，-\frac{1}{2}）$ |
4．设集合M={x|$\frac{1}{2}≤x＜3$}，函数f（x）=ln（1-$\sqrt{x}$）的定义域为N，则M∩N为（ ）
| A． | [$\frac{1}{2}$，1] | B． | [$\frac{1}{2}$，1） | C． | （0，$\frac{1}{2}$] | D． | （0，$\frac{1}{2}$） |