题目内容
20．已知椭圆$\frac{{x}^{2}}{9+k}$+$\frac{{y}^{2}}{5-k}$=1的离心率为$\frac{1}{2}$，则实数k的值为（ ）| A． | -1 | B． | 47 | C． | -1或-3 | D． | -1或3 |
分析 利用椭圆的离心率，列出方程求解即可．
解答 解：当焦点在x轴时，椭圆$\frac{{x}^{2}}{9+k}$+$\frac{{y}^{2}}{5-k}$=1的离心率为$\frac{1}{2}$，
可得：$\frac{4+2k}{9+k}$=$\frac{1}{4}$，解得k=-1；
当焦点在y轴时，椭圆$\frac{{x}^{2}}{9+k}$+$\frac{{y}^{2}}{5-k}$=1的离心率为$\frac{1}{2}$，
可得：$\frac{-4-2k}{5-k}=\frac{1}{4}$，解得k=-3；
所以k的取值为：-1或-3．
故选：C．
点评 本题考查椭圆的简单性质的应用，注意椭圆的焦点所在轴，是易错点．
练习册系列答案
相关题目
16．已知集合A={-3，-2，-1，0，1，2}，B={x|（x+3）（x-1）＜0}，则A∩B=（ ）
| A． | {0，1，2} | B． | {-2，-1，0} | C． | {-3，-2，-1，0，1} | D． | {0，1，2，3} |
如图，在△OAB中，$\overrightarrow{OC}$=$\frac{1}{4}$$\overrightarrow{OA}$，$\overrightarrow{OD}$=$\frac{1}{2}$$\overrightarrow{OB}$，AD与BC交于点M，设$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$．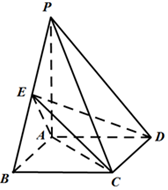
如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA垂直底面ABCD，PA=AB=2，E是棱PB的中点．
12．设函数f（x）=t|x-t|（t≠0）在区间（-∞，-1]上单调递增，则t的取值范围是（ ）
| A． | （-∞，-1] | B． | [-1，0） | C． | （0，1] | D． | [1，+∞） |