题目内容
已知函数f (x)=x2,g(x)=x-1.
(x)=x2,g(x)=x-1.
(1)若存在x∈R使f(x)<b·g(x),求实数b 的取值范围;
的取值范围;
(2)设F(x)=f(x)-mg(x)+1-m-m2,且|F(x)|在[0,1]上单调递增,求实数m的取值范围.
解 (1)∃x∈R,f(x)<bg(x)⇒∃x∈R,x2-bx+b<0
⇒(-b)2-4b>0⇒b<0或b>4.
(2)F(x)=x2-mx+1-m2, Δ=m2-4(1-m2)=5m2-4.
Δ=m2-4(1-m2)=5m2-4.
①当Δ≤0,即- ≤m≤
≤m≤ 时,则必需
时,则必需
 ⇒-
⇒- ≤m≤
≤m≤ 0.
0.
②当Δ>0,即m<- 或m>
或m> 时,设方程F(x)=0的根为x1,x2(x1<x2).
时,设方程F(x)=0的根为x1,x2(x1<x2).
若 ≥1,则x1≤0,即
≥1,则x1≤0,即 ⇒m≥2;
⇒m≥2;
若 ≤0,则x2≤0,即
≤0,则x2≤0,即
⇒-1≤m<- ;
;
综上所述:-1≤m≤0或m≥2.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
 ,P={x|a+1<x<2a+15}.
,P={x|a+1<x<2a+15}. 价调至0.55
价调至0.55 ,其图象关于点(-3,2)对称,则f(2)的值是____
,其图象关于点(-3,2)对称,则f(2)的值是____ ____.
____. =
= ,则a=________.
,则a=________.
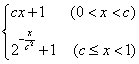 满足f(c2)=
满足f(c2)= .
. +1.
+1.