题目内容
已知α、β是不同的平面,m、n是不同的直线,给出下列命题:
①若
②若 则
则
③如果 ,m、n是异面直线,那么n与α相交。
,m、n是异面直线,那么n与α相交。
④若 ,则n//α且n//β。
,则n//α且n//β。
其中正确命题的个数是( )
| A.4 | B.3 | C.2 | D.1 |
C
解析试题分析:①若 正确,因为,一个平面如果经过另一平面的一条垂线,那么这两个平面垂直。
正确,因为,一个平面如果经过另一平面的一条垂线,那么这两个平面垂直。
②若 则
则 。不正确,只有当m,n是相交直线时,才成立。
。不正确,只有当m,n是相交直线时,才成立。
③如果 ,m、n是异面直线,那么n与α相交。不正确,有可能n与α平行。
,m、n是异面直线,那么n与α相交。不正确,有可能n与α平行。
④若 ,则n//α且n//β。正确,由线面平行的判定定理可知。
,则n//α且n//β。正确,由线面平行的判定定理可知。
故选C。
考点:本题主要考查立体几何中的平行关系、垂直关系。
点评:基础题,高考题中,立体几何往往是一大二小,其中像这类题目比较多见。关键是有关定理要熟悉。命题真假的判断,可采用举反例的方法,说明其不成立。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设m,n是异面直线,则(1)一定存在平面α,使m α,且n∥α;(2)一定存在平面α,使m
α,且n∥α;(2)一定存在平面α,使m α,且n⊥α;(3)一定存在平面γ,使得m,n到平面γ距离相等;(4)一定存在无数对平面α和β,使m
α,且n⊥α;(3)一定存在平面γ,使得m,n到平面γ距离相等;(4)一定存在无数对平面α和β,使m α,n
α,n β且α⊥β。上述4个命题中正确命题的序号是( )
β且α⊥β。上述4个命题中正确命题的序号是( )
| A.(1)(2)(3) | B.(1)(2)(4) | C.(1)(3)(4) | D.(1)(4) |
已知 ,
, ,
,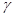 是三个互不重合的平面,
是三个互不重合的平面, 是一条直线,下列命题中正确命题是( )
是一条直线,下列命题中正确命题是( )
A.若 , , ,则 ,则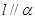 | B.若 上有两个点到 上有两个点到 的距离相等,则 的距离相等,则 |
C.若 , , ∥ ∥ ,则 ,则 | D.若 , , ,则 ,则 |
若 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,则下列命题中的真命题是( )
是三个不同的平面,则下列命题中的真命题是( )
A.若 ,则 ,则 | B. |
C.若 , , ,则 ,则 | D.若 , , ,则 ,则 |
如图在三棱锥 中,E?F是棱AD上互异的两点,G?H是棱BC上互异的两点,由图可知
中,E?F是棱AD上互异的两点,G?H是棱BC上互异的两点,由图可知
①AB与CD互为异面直线;②FH分别与DC?DB互为异面直线;
③EG与FH互为异面直线;④EG与AB互为异面直线.
其中叙述正确的是 ( )
| A.①③ | B.②④ | C.①②④ | D.①②③④ |
在正方体 中,下面结论错误的是( )
中,下面结论错误的是( )
A.BD//平面 | B. |
C. | D.异面直线AD与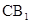 所成角为450 所成角为450 |
在长方体 中,
中, =2
=2 ,
, =
= ,则二面角
,则二面角 的大小是 ( )
的大小是 ( )
| A.300 | B.450 | C.600 | D.900 |




