题目内容
已知f(x)=
-
,求:
(1)f(x)的定义域;
(2)化简解析式;
(3)求f(2).
| x+x-1 |
| x-x-1 |
x
| ||||
x
|
(1)f(x)的定义域;
(2)化简解析式;
(3)求f(2).
考点:函数的定义域及其求法,根式与分数指数幂的互化及其化简运算
专题:函数的性质及应用
分析:(1)直接根据分式函数,分母不为零,列出不等式组进行求解;
(2)根据幂的运算性质进行求解;
(3)将x=2代人直接求解即可.
(2)根据幂的运算性质进行求解;
(3)将x=2代人直接求解即可.
解答:
解:(1)据题,得
,
解得:x∈(0,1)∪(1,+∞),
∴f(x)的定义域(0,1)∪(1,+∞);
(2)∵f(x)=
-
=
-
=
,
∴f(x)=
,
(3)∵f(x)=
,
∴f(2)=-
.
|
解得:x∈(0,1)∪(1,+∞),
∴f(x)的定义域(0,1)∪(1,+∞);
(2)∵f(x)=
| x+x-1 |
| x-x-1 |
x
| ||||
x
|
=
| x2+1 |
| x2-1 |
| x+1 |
| x-1 |
=
| 2x |
| 1-x2 |
∴f(x)=
| 2x |
| 1-x2 |
(3)∵f(x)=
| 2x |
| 1-x2 |
∴f(2)=-
| 4 |
| 3 |
点评:本题综合考查了函数的定义域、解析式、函数值的求解方法,属于中档题,解题关键是,准确领悟常见函数的定义域问题,函数的解析式的化简等知识灵活运用.

练习册系列答案
相关题目
四棱锥的底面是边长为6的正方形,侧面是全等的等腰三角形,侧棱长为5,则其表面积为( )
| A、36 | B、72 | C、84 | D、96 |
已知a=100×99×98×97×96×95,则a=( )
| A、A1005 |
| B、C1005 |
| C、A1006 |
| D、C1006 |
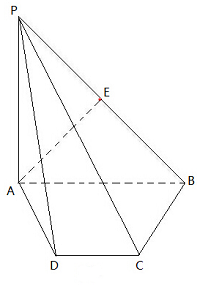 在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,PA⊥底面ABCD,E为PB中点,PA=a.
在四棱锥P-ABCD中,底面ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,PA⊥底面ABCD,E为PB中点,PA=a.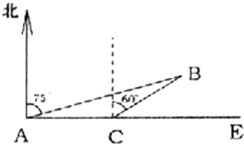 2008年2月26日,中国海军三艘舰艇从海南省三亚启航赴亚丁湾、索马里海域执行首次护航任务,是我国15世纪后最大远征.参与此次护航任务的舰艇有169“武汉”号导弹驱逐舰、171“海口”号导弹驱逐舰、887“微山湖”号综合补给舰.假设护航编队在索马里海域执行护航任务时(如图),海中有一小岛,周围3.8海里内有暗礁.军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北端东60°.若此舰不改变舰行的方向继续前进,问此舰有没有角礁的危险?
2008年2月26日,中国海军三艘舰艇从海南省三亚启航赴亚丁湾、索马里海域执行首次护航任务,是我国15世纪后最大远征.参与此次护航任务的舰艇有169“武汉”号导弹驱逐舰、171“海口”号导弹驱逐舰、887“微山湖”号综合补给舰.假设护航编队在索马里海域执行护航任务时(如图),海中有一小岛,周围3.8海里内有暗礁.军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北端东60°.若此舰不改变舰行的方向继续前进,问此舰有没有角礁的危险?