题目内容
设a＞0，b＞0．，且a+b=1，则
+
的最小值为
| 1 |
| a |
| 1 |
| b |
4
4
．分析：根据基本不等式的应用，即可求
+
的最小值．
| 1 |
| a |
| 1 |
| b |
解答：解：∵a+b=1，
∴
+
=（a+b）（
+
）=2+
+
≥2+2
=4，
当且仅当
=
，即a=b=
时，取等号．
故答案为：4．
∴
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| b |
| a |
| a |
| b |
|
当且仅当
| b |
| a |
| a |
| b |
| 1 |
| 2 |
故答案为：4．
点评：本题主要考查基本不等式的应用，注意基本不等式成立的三个条件．
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
．
），f（
）是否成等比数列，并证明f（
）≤f（
）；
为a、b的调和平均数，记为H．若H≤f（x）≤G，求x的取值范围．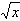
，g（x）=alnx，a∈R。
。
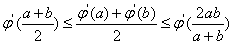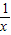＜b的解集为（ ）
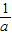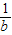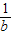，0）∪（0，
）
，-
）
，0）∪（0，-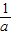
）
）∪（
，+∞）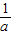