题目内容
在等差数列{an}中,a4=-15,公差d=3,求数列an的前n项和为Sn的最小值.
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由已知条件利用等差数列通项公式求出首项,从而求出前n项和,利用配方法能求出结果.
解答:
解:∵在等差数列{an}中,a4=-15,公差d=3,
a1=-15-3×3=-24,
∴Sn=-24n+
×3
=
(n2-17n)
=
(n-
)2-
,
∴n=8或n=9时,Sn取最小值-108.
a1=-15-3×3=-24,
∴Sn=-24n+
| n(n-1) |
| 2 |
=
| 3 |
| 2 |
=
| 3 |
| 2 |
| 17 |
| 2 |
| 867 |
| 8 |
∴n=8或n=9时,Sn取最小值-108.
点评:本题考查等差数列的前n项和的最小值的求法,是基础题,解题时要注意等差数列的性质的合理运用.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
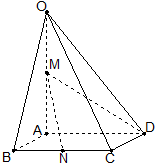 如图,在四棱锥O-ABCD中,底面ABCD是边长为1的菱形,∠ABC=
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的菱形,∠ABC= 请你设计一个LED霓虹灯灯箱.现有一批LED霓虹灯灯箱材料如图所示,ABCD是边长为60cm的正方形LED散片,边CD上有一以其中点M为圆心,半径为2cm的半圆形缺损,因此切去阴影部分(含半圆形缺损)所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于空间一点P,正好形成一个正四棱柱形状有盖的LED
请你设计一个LED霓虹灯灯箱.现有一批LED霓虹灯灯箱材料如图所示,ABCD是边长为60cm的正方形LED散片,边CD上有一以其中点M为圆心,半径为2cm的半圆形缺损,因此切去阴影部分(含半圆形缺损)所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于空间一点P,正好形成一个正四棱柱形状有盖的LED 双曲线
双曲线