Question

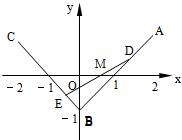如图，三定点A（2，1），B（0，-1），C（-2，1）；三动点D，E，M满足

AD

=t

AB

，

BE

=t

BC

，

DM

=t

DE

，t∈[0，1]．
（Ⅰ）求动直线DE斜率的变化范围；
（Ⅱ）求动点M的轨迹方程．

Answer 1

分析：（Ⅰ）设出D，E，M三点的坐标，由三动点D，E，M满足

AD

=t

AB

，

BE

=t

BC

，转化成坐标表示，求出D，E的用参数表示的坐标．将斜率表示成参数t的函数，再用函数的单调性求出斜率的范围．
（2）方法一：由

DM

=t

DE

，利用向量相等的条件得出点M的坐标关于参数t的方程，消参得出点M的横纵坐标满足的方程，即动点M的轨迹方程．
方法二：与方法一原理一样是得到点M的坐标关于参数t的方程，只是其在找到坐标之间关系时没有用（I）的结论，而是全部用向量的方法，找到了点M的坐标与参数t的关系，此法较繁琐．

解答：解法一：如图，（Ⅰ）设D（x₀，y₀），E（x_E，y_E），M（x，y）．
由

AD

=t

AB

，

BE

=t

BC

，知（x_D-2，y_D-1）=t（-2，-2）．
∴

xD=-2t+2 yD=-2t+1

同理

xE=-2t yE=2t-1

．
∴k_DE=

yE-yD

xE-xD

=

2t-1-(-2t+1)

-2t-(-2t+2)

=1-2t．
∵t∈[0，1]，∴k_DE∈[-1，1]．

（Ⅱ）∵

DM

=t

DE

∴（x+2t-2，y+2t-1）=t（-2t+2t-2，2t-1+2t-1）=t（-2，4t-2）=（-2t，4t²-2t）．
∴

x=2(1-2t) y=(1-2t)2

，
∴y=

x2

4

，即x²=4y．
∵t∈[0，1]，x=2（1-2t）∈[-2，2]．
即所求轨迹方程为：x²=4y，x∈[-2，2]

解法二：（Ⅰ）同上．
（Ⅱ）如图，

OD

=

OA

+

AD

=

OA

+t

AB

=

OA

+t（

OB

-

OA

）=（1-t）

OA

+t

OB

，

OE

=

OB

+

BE

=

OB

+t

BC

=

OB

+t（

OC

-

OB

）=（1-t）

OB

+t

OC

，

OM

=

OD

+

DM

=

OD

+t

DE

=

OD

+t（

OE

-

OD

）=（1-t）

OD

+t

OE

=（1-t²）

OA

+2（1-t）t

OB

+t²

OC

．
设M点的坐标为（x，y），由

OA

=（2，1），

OB

=（0，-1），

OC

=（-2，1）得

x=(1-t2)•2+2(1-t)t•0+t2•(-2)=2(1-2t) y=(1-t)2•1+2(1-t)t•(-1)+t2•1=(1-2t)2

消去t得x²=4y，
∵t∈[0，1]，x∈[-2，2]．
故所求轨迹方程为：x²=4y，x∈[-2，2]

点评：考查向量相等的充要条件与求轨迹方程时先求参数方程的思路，此类题在消参数时应注意观察形式，找到一个消去参数的好的方法．在方法二中连续使用向量的三角形法则变形，一定要细心哟！