题目内容
5.设直线3x-4y+5=0的倾斜角为α.(1)求tan2α的值;
(2)求$cos({\frac{π}{6}-α})$的值.
分析 (1)求出倾斜角的正切函数值,利用二倍角的正切函数公式即可计算得解.
(2)利用同角三角函数的基本关系式求解sinα,cosα的值,进而利用两角差的余弦函数公式即可计算得解.
解答 解:(1)直线3x-4y+5=0的倾斜角为α,可得tanα=$\frac{3}{4}$,α是锐角.
可得:tan2α=$\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{24}{7}$.
(2)∵tanα=$\frac{3}{4}$=$\frac{sinα}{cosα}$,α是锐角,
又∵sin2α+cos2α=1,
∴解得sinα=$\frac{3}{5}$.cos$α=\frac{4}{5}$,
∴$cos({\frac{π}{6}-α})$=$\frac{\sqrt{3}}{2}×\frac{4}{5}$+$\frac{1}{2}×\frac{3}{5}$=$\frac{3+4\sqrt{3}}{10}$.
点评 本题考查直线的倾斜角与同角三角函数的基本关系式,两角差的余弦函数公式的应用,考查计算能力.

练习册系列答案
相关题目
20.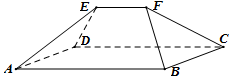 《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体(如图):面ABCD为矩形,棱EF∥AB.若此几何体中,AB=4,EF=2,△ADE和△BCF都是边长为2的等边三角形,则此几何体的表面积为( )
《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体(如图):面ABCD为矩形,棱EF∥AB.若此几何体中,AB=4,EF=2,△ADE和△BCF都是边长为2的等边三角形,则此几何体的表面积为( )
 《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体(如图):面ABCD为矩形,棱EF∥AB.若此几何体中,AB=4,EF=2,△ADE和△BCF都是边长为2的等边三角形,则此几何体的表面积为( )
《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体(如图):面ABCD为矩形,棱EF∥AB.若此几何体中,AB=4,EF=2,△ADE和△BCF都是边长为2的等边三角形,则此几何体的表面积为( )| A. | $8\sqrt{3}$ | B. | $8+8\sqrt{3}$ | C. | $6\sqrt{2}+2\sqrt{3}$ | D. | $8+6\sqrt{2}+2\sqrt{3}$ |
17.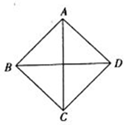 已知某几何体是由两个四棱锥组合而成,若该几何体的正视图、俯视图和侧视图均为如图所示的图形,其中四边形是边长为$\sqrt{2}$的正方形,则该几何体的表面积是( )
已知某几何体是由两个四棱锥组合而成,若该几何体的正视图、俯视图和侧视图均为如图所示的图形,其中四边形是边长为$\sqrt{2}$的正方形,则该几何体的表面积是( )
 已知某几何体是由两个四棱锥组合而成,若该几何体的正视图、俯视图和侧视图均为如图所示的图形,其中四边形是边长为$\sqrt{2}$的正方形,则该几何体的表面积是( )
已知某几何体是由两个四棱锥组合而成,若该几何体的正视图、俯视图和侧视图均为如图所示的图形,其中四边形是边长为$\sqrt{2}$的正方形,则该几何体的表面积是( )| A. | 8$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{3}$+2 | D. | 4$\sqrt{3}$+2 |