题目内容
已知异面直线a,b均与平面α相交,下列命题:
①存在直线m?α,使得m⊥a或m⊥b;
②存在直线m?α,使得m⊥a且m⊥b;
③存在直线m?α,使得m与a和b所成的角相等.
其中不正确的命题个数为( )
①存在直线m?α,使得m⊥a或m⊥b;
②存在直线m?α,使得m⊥a且m⊥b;
③存在直线m?α,使得m与a和b所成的角相等.
其中不正确的命题个数为( )
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:根据空间线线关系,线面关系,线线夹角,线线垂直的几何特征,逐一分析四个答案的真假,可得答案.
解答:
解:根据空间线线垂直的几何特征可得:
必存在直线m?α,使得m⊥a,
也必存在直线m?α,使得m⊥b,
故①正确;
若异面直线a,b的公垂线段与平面α平行或在平面α内,
则存在直线m?α,使得m⊥a且m⊥b,
否则这样的m不存在,
故②错误;
若异面直线a,b中有一条与平面α垂直,则
平面α内另一条直线的垂线与两条直线均垂直;
若异面直线a,b与平面α均不垂直,则它们在平面α上射影的角平分线与异面直线a,b夹角相等,
故③正确.
故①③都正确,
故不正确的命题个数为1,
故选:B
必存在直线m?α,使得m⊥a,
也必存在直线m?α,使得m⊥b,
故①正确;
若异面直线a,b的公垂线段与平面α平行或在平面α内,
则存在直线m?α,使得m⊥a且m⊥b,
否则这样的m不存在,
故②错误;
若异面直线a,b中有一条与平面α垂直,则
平面α内另一条直线的垂线与两条直线均垂直;
若异面直线a,b与平面α均不垂直,则它们在平面α上射影的角平分线与异面直线a,b夹角相等,
故③正确.
故①③都正确,
故不正确的命题个数为1,
故选:B
点评:本题考查的知识点空间线线关系,线面关系,线线夹角,线线垂直的几何特征,难度不大,属于基础题.

练习册系列答案
相关题目
若α=390°,则角α的终边落在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设集合P={x|x2-2
x≤0},m=20.3,则下列关系中正确的是( )
| 3 |
| A、m⊆P | B、m∉P |
| C、{m}∈P | D、{m}?P |
如果幂函数y=(n2-3n+3)xn2-n-2的图象不过原点,则取n值为( )
| A、n=1或n=2 |
| B、n=1或n=0 |
| C、n=1 |
| D、n=2 |
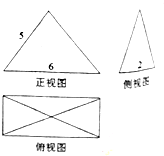 一个何体的三视图如图所示,其中正视图是底边长为6,腰长为5的等腰三角形,侧视图是底边长为2的等腰三角影,则该几何体的体积为( )
一个何体的三视图如图所示,其中正视图是底边长为6,腰长为5的等腰三角形,侧视图是底边长为2的等腰三角影,则该几何体的体积为( )| A、16 | B、24 | C、32 | D、48 |