题目内容
假设关于某种设备的使用年限x(年)与所支出的维修费用y(万元),有如下统计资料:
①对x、y进行线性相关性检验;
②如果x、y具有线性相关关系,求出线性回归方程;
③估计使用年限为8年,维修费用约是多少?
b=
,r=
(已知:
xi2=90,
yi2=140.8,
xiyi=112.3,
≈8.9,
≈1.4)
| X | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
②如果x、y具有线性相关关系,求出线性回归方程;
③估计使用年限为8年,维修费用约是多少?
b=
| |||||||
|
| ||||||||||||||||||
|
(已知:
| s |
 |
| i=1 |
| s |
 |
| i=1 |
| s |
 |
| i=1 |
| 79 |
| 2 |
考点:回归分析
专题:应用题,概率与统计
分析:①由题意,r=
≈0.987,故有较强的线性相关关系;
②根据所给的数据,做出变量x,y的平均数,根据最小二乘法做出线性回归方程的系数b,再根据样本中心点一定在线性回归方程上,求出a的值,写出线性回归方程;
③当自变量为8时,代入线性回归方程,求出维修费用,这是一个预报值.
| 112.3-5•4•5 | ||||
|
②根据所给的数据,做出变量x,y的平均数,根据最小二乘法做出线性回归方程的系数b,再根据样本中心点一定在线性回归方程上,求出a的值,写出线性回归方程;
③当自变量为8时,代入线性回归方程,求出维修费用,这是一个预报值.
解答:
解:①由题意,r=
≈0.987,故有较强的线性相关关系;
②b=
,a=5-1.23×4=0.08,
∴y=1.23x+0.08
③当x=8时,y=1.23×8+0.08=9.92万元.
| 112.3-5•4•5 | ||||
|
②b=
| 112.3-5•4•5 |
| 90-5•42 |
∴y=1.23x+0.08
③当x=8时,y=1.23×8+0.08=9.92万元.
点评:本题考查线性回归方程的求解和应用,是一个基础题,解题的关键是正确应用最小二乘法来求线性回归方程的系数.

练习册系列答案
相关题目
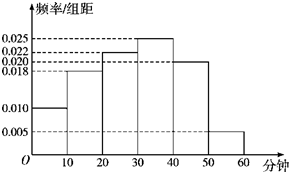 我校为了了解高二级学生参加体育活动的情况,随机抽取了100名高二级学生进行调查.如图是根据调查结果绘制的学生日均参加体育活动时间的频率分布直方图.将日均参加体育活动时间不低于40分钟的学生称为参加体育活动的“积极分子”.根据已知条件完成下面的列联表,并据此资料,在犯错误的概率不超过5%的前提下,你是否认为参加体育活动的“积极分子”与性别有关?
我校为了了解高二级学生参加体育活动的情况,随机抽取了100名高二级学生进行调查.如图是根据调查结果绘制的学生日均参加体育活动时间的频率分布直方图.将日均参加体育活动时间不低于40分钟的学生称为参加体育活动的“积极分子”.根据已知条件完成下面的列联表,并据此资料,在犯错误的概率不超过5%的前提下,你是否认为参加体育活动的“积极分子”与性别有关?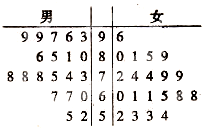 在某次数学考试中,从高一年级300名男生和300名女生中,各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示:
在某次数学考试中,从高一年级300名男生和300名女生中,各随机抽取20名学生的成绩进行统计,作出茎叶图如图所示: