Question

2．定义a⊕b=$\left\{\begin{array}{l}{a（a≥b）}\\{b（a＜b）}\end{array}\right.$．若f（x）=cosx⊕（$\frac{\sqrt{2}}{2}$tanx）（-$\frac{π}{2}$＜x＜$\frac{π}{2}$）．
（1）求函数f（x）的单调区间；
（2）若方程f（x）-$\frac{1}{sinα}$=0有解，求实数α的取值范围．

Answer 1

分析 （1）根据新定义进行比较，求出函数的解析式．
（2）根据函数与方程之间的关系转化为两个函数图象的相交问题．

解答 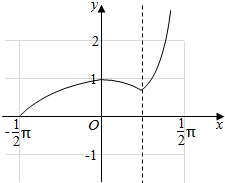解：（1）若cosx≥$\frac{\sqrt{2}}{2}$tanx，
即cos²x≥$\frac{\sqrt{2}}{2}$sinx，
即1-sin²x≥$\frac{\sqrt{2}}{2}$sinx，
即sin²x+$\frac{\sqrt{2}}{2}$sinx-1≤0，
即2sin²x+$\sqrt{2}$sinx-2≤0，
解得-$\sqrt{2}$≤sinx≤$\frac{\sqrt{2}}{2}$，
即-1＜sinx≤$\frac{\sqrt{2}}{2}$，此时-$\frac{π}{2}$＜x≤$\frac{π}{4}$．
当$\frac{π}{4}$＜x＜$\frac{π}{2}$时，cosx＜$\frac{\sqrt{2}}{2}$tanx，
即f（x）=$\left\{\begin{array}{l}{cosx，}&{-\frac{π}{2}＜x≤\frac{π}{4}}\\{\frac{\sqrt{2}}{2}tanx，}&{\frac{π}{4}＜x＜\frac{π}{2}}\end{array}\right.$．作出f（x）的图象，则函数单调递增区间为（-$\frac{π}{2}$，0]，（$\frac{π}{4}$，$\frac{π}{2}$）．
（2）若方程f（x）-$\frac{1}{sinα}$=0有解，
则等价为若方程f（x）=$\frac{1}{sinα}$有解，
即函数f（x）与y=$\frac{1}{sinα}$有交点，
∵f（x）＞0，
∴$\frac{1}{sinα}$＞0，即sinα＞0，
则2kπ＜α＜2kπ+π，k∈Z．

点评 本题主要考查三角函数的图象和性质，利用数形结合是解决本题的关键．考查学生的运算和推理能力．