题目内容
中心在原点、焦点在x轴上的椭圆C的一个顶点为B(0,-1),右焦点到直线m:x-y+2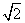 =
= 0的距离为3.
0的距离为3.
(1)求椭圆C的标准方程;
(2)是否存在斜率k≠0的直线l与C交于M,N两点,使|BM|=|BN|?若存在,求k的取值范围;若不存在,说明理由.
解:(1)由题意,b2=1,设右焦点为F(c,0),
则d= =3,即|c+2
=3,即|c+2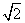 |=3
|=3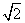 .
.
解 得c=
得c=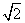 ,又a2=c2+b2=3,∴a2=3.
,又a2=c2+b2=3,∴a2=3.
∴所求椭圆C的标准方程为 +y2=1.
+y2=1.
(2)假设存在k满足条件,设l与C的交点为M(x1,y1),N(x2,y2).
则 两式相减得
两式相减得
 (x1+x2)(x1-x2)+(y1+y2)(y1-y2)=0.
(x1+x2)(x1-x2)+(y1+y2)(y1-y2)=0.
设MN的中点为P(x0,y0),∴k·kOP=- ,
,
 ∵要使|BM|=|BN|,需
∵要使|BM|=|BN|,需 +y
+y <1.
<1.
 ∴k2<1且k≠0.
∴k2<1且k≠0.
∴存在-1<k<0或0<k<1满足题设.

练习册系列答案
相关题目
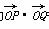 =-2,求实数k的值;
=-2,求实数k的值; B.1
B.1 D.
D.
 ,则动点Q的轨迹方程为________.
,则动点Q的轨迹方程为________. +y2=1相交于A、B两点,则|AB|的最大值为( )
+y2=1相交于A、B两点,则|AB|的最大值为( )
 D.
D.
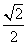 的椭圆C:
的椭圆C: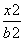 +
+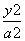 =1(a>b>0)上的一点,斜率为
=1(a>b>0)上的一点,斜率为 在点
在点 处的切线平行于
处的切线平行于 轴,则
轴,则 的值为 ( )
的值为 ( ) B.
B. C.
C. D.
D.
 B.60
B.60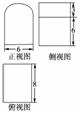
 :
: ,使得
,使得 ,则命题
,则命题 是( )
是( ) ,都有
,都有 B.
B.  ,使得
,使得 D.
D.