题目内容
12.函数y=$\frac{1}{x+1}$的图象与函数y=2sinπx(-4≤x≤2)的图象所有交点的横坐标之和等于-4.分析 先求出函数y=-$\frac{1}{x}$的图象向右平移1个单位之后得到的函数解析式,分别作出两个函数的图象,根据图象的对称性即可得到交点坐标问题.
解答 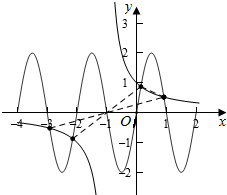 解:作出函数y=$\frac{1}{x+1}$的图象,则函数关于点(-1,0)对称,
解:作出函数y=$\frac{1}{x+1}$的图象,则函数关于点(-1,0)对称,
同时点(-1,0)也是函数y=2sinπx(-4≤x≤2)的对称点,
由图象可知,两个函数在[-4,2]上共有4个交点,两两关于点(-1,0)对称,
设对称的两个点的横坐标分别为x1,x2,
则x1+x2=2×(-1)=-2,
∴4个交点的横坐标之和为2×(-2)=-4.
故答案为:-4
点评 本题主要考查函数交点个数以及数值的计算,根据函数图象的性质,利用数形结合是解决此类问题的关键,难度较大,综合性较强.

练习册系列答案
相关题目
20.已知a∈R,则“|a-1|+|a|≤1”是“函数y=ax在R上为减函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.已知F1、F2是椭圆E:$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{m}^{2}-1}$=1(m>1)的左、右焦点,设椭圆E的离心率为e,若在椭圆E上存在点P使得|PF1|2+|PF2|2=4m,则e+$\frac{1}{e}$的取值范围为( )
| A. | (2,5] | B. | ($\frac{5}{2}$,3] | C. | (2,$\frac{5}{2}$] | D. | (2,$\frac{5}{2}$) |
4.空间四边形ABCD中,AB、BC、CD的中点是P、Q、R,PQ=3,QR=4,PR=5,那么异面直线AC、BD所成的角是( )
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |