题目内容
(1)用辗转相除法求9322与6903的最大公约数;
(2)用更相减损术求168与105的最大公约数.
(2)用更相减损术求168与105的最大公约数.
考点:用辗转相除计算最大公约数
专题:算法和程序框图
分析:(1)根据辗转相除法的步骤,将9322与6903代入易得到答案.
(2)根据“以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数.继续这个操作,直到所得的减数和差相等为止.”的原则,易求出168与105的最大公约数.
(2)根据“以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数.继续这个操作,直到所得的减数和差相等为止.”的原则,易求出168与105的最大公约数.
解答:
解:(1)(5分)∵9322=6903×1+2419,6903=2419×2+2065,2419=2065×1+354
2065=354×5+295,354=295×1+59,295=59×5,∴9322与6903的最大公约数是59;
(2)(5分)∵168-105=63,105-63=42,63-42=21,42-21=21,
∴168与105的最大公约数是21.
2065=354×5+295,354=295×1+59,295=59×5,∴9322与6903的最大公约数是59;
(2)(5分)∵168-105=63,105-63=42,63-42=21,42-21=21,
∴168与105的最大公约数是21.
点评:本题考查的知识点是辗转相除法,对任意整数a,b,b>0,存在唯一的整数q,r,使a=bq+r,其中0≤r<b,这个事实称为带余除法定理,若c|a,c|b,则称c是a,b的公因数.若d是a,b的公因数,且d可被a,b的任意公因数整除则称d是a,b的最大公因数.当d≥0时,d是a,b公因数中最大者.若a,b的最大公因数等于1,则称a,b互素.累次利用带余除法可以求出a,b的最大公因数,这种方法常称为辗转相除法.更相减损术的方法和步骤是:以较大的数减较小的数,接着把所得的差与较小的数比较,并以大数减小数.继续这个操作,直到所得的减数和差相等为止.

练习册系列答案
相关题目
已知数列{an}满足:a1=1,
=
,n∈N*,{an}的前项和为Sn,则( )
| 1 |
| an+1 |
| 1 |
| 2an |
A、Sn=2-(
| ||
B、Sn=2-(
| ||
| C、Sn=2n-1 | ||
| D、Sn=2n-1-1 |
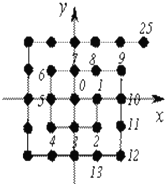 将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,…,点(0,1)处标7,…,依此类推,则标签20152的格点的坐标为( )
将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签:原点处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,…,点(0,1)处标7,…,依此类推,则标签20152的格点的坐标为( )| A、(1008,1007) |
| B、(1007,1006) |
| C、(1007,1005) |
| D、(1006,1005) |
下列是映射的是( )


| A、1、2、3 | B、1、2 |
| C、1、3 | D、2、3 |
二进制数1111111111转化为十进制数应该是( )
| A、1023 | B、1024 |
| C、2047 | D、2048 |
