题目内容

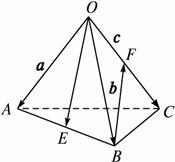
空间四边形OABC,各边及对角线长都相等,E、F分别为AB、OC的中点，求OE与BF所成的角.

解：如图，设=a，=b，=c，且|a|=|b|=|c|=1，易知∠AOB=∠BOC=∠AOC=，则a·b=b·c=c·a=.?

∵=(a+b),=c-b,| |=||=,?

∴=（a+b）（c-b）?

=ac+bc-ab-|b|2=-，?

∴cos〈，〉==-，?

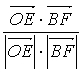∴〈，〉=π-arccos.?

因此,异面直线OE与BF所成的角为arccos.


练习册系列答案
相关题目
空间四边形OABC中，OB=OC，∠AOB=∠AOC=
π
3
，则cos＜
OA
，
BC
＞的值是（　　）
A、
1
2
B、
2
2
C、-
1
2
D、0
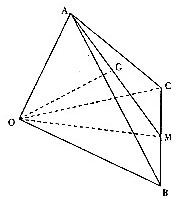精英家教网如图，在空间四边形OABC中，M，G分别是BC，AM的中点，设
OA
=
a
，
OB
=
b
，
OC
=
c
．
（1）用基底{
a
 ， 
b
 ，
c
}表示向量
OG
；
（2）若|
a
|=|
b
|=|
c
|=
3
，且
a
与
b
、
c
夹角的余弦值均为
1
3
，
b
与
c
夹角为60°，求|
OG
|．
已知空间四边形OABC，M，N分别是OA，BC的中点，且
OA
=
a
，
OB
=
b
，
OC
=
c
，用
a
，
b
，
c
表示向量
MN
为（　　）
在空间四边形OABC中，OA=8，AB=6，AC=4，BC=5，∠OAC=45°，∠OAB=60°．则异面直线AO与BC的夹角的余弦值为
1
5
(3-2
2
)
1
5
(3-2
2
)
．
空间四边形OABC中，
OA
=
a
，
OB
=
b
，
OC
=
c
，点M在OA上，且OM=2MA，N为BC的中点，则
MN
=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网