Question

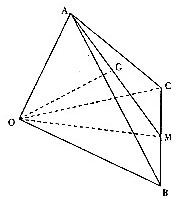如图，在空间四边形OABC中，M，G分别是BC，AM的中点，设

OA

=

a

，

OB

=

b

，

OC

=

c

．
（1）用基底{

a

 ， 

b

 ，

c

}表示向量

OG

；
（2）若|

a

|=|

b

|=|

c

|=

3

，且

a

与

b

、

c

夹角的余弦值均为

1

3

，

b

与

c

夹角为60°，求|

OG

|．

Answer 1

分析：（1）根据所给的图形和一组基底，从起点O出发，利用向量和的三角形法则，把不是基底中的向量再用是基地的向量来表示，做出结果．
（2）欲求向量的模，可先将模平方，根据公式|

a

| 2=

a

 2，再将平方式展开结合向量的数量积求出其值即可．

解答：解：（1）

OG

=

1

2

（

OA

+

OM

）
  

OM

=

1

2

（

OB

+

OC

）
∴

OG

=

1

2

OA

+

1

4

OB

+

1

4

OC

，
即

OG

=

1

2

a

+

1

4

b

+

1

4

c

（2）|

OG

|²=（

1

2

a

+

1

4

b

+

1

4

c

）^2
=

1

16

（4

a2

+

b2

+

c2

+4

ab

+4

ac

+2

bc

）
又|

a

|=|

b

|=|

c

|=

3

，
cos＜

a

，

b

＞=cos＜

a

，

c

＞=

1

3

，cos＜

b

，

c

＞=cos60°=

1

2

∴|

OG

|2=

1

16

（4×3+3+3+4+4+3）=

29

16

∴|

OG

|=

29

4

．

点评：本题考查向量在几何中的应用、向量的加法法则，还考查向量的基本定理及其意义，解题时注意方法，即从要表示的向量的起点出发，沿着空间图形的棱走到终点，若出现不是基底中的向量的情况，再重复这个过程，是基础题．