Question

（1）作出y=lg|x|的图象，并指出单调区间；

（2）作出y=|lgx|的图象，并指出单调区间.

Answer 1

解析：（1）∵f(-x)

    =lg|(-x)|

    =lg|x|=f(x),

    ∴f(x)是偶函数,其图象关于y轴对称.先画出x＞0时的图象,再利用其对称性完成整个函数的图象.

f(x)=lg|x|=如下图，

   

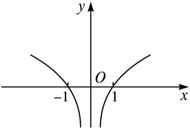
∴f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增.

    （2）当lgx≥0，即x≥1时，y=lgx；

    当lgx＜0，即0＜x＜1时，y=-lgx.

    其图象如下图：

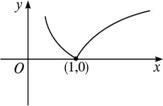
    由图象可知其单调增区间为［1，+∞），单调减区间为（0，1］.