题目内容
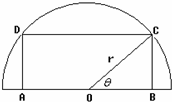 如图,在一个半径为r的半圆形铁板中有一个内接矩形ABCD,矩形的边AB在半圆的直径上,顶点C、D在半圆上,O为圆心.令∠BOC=θ,用θ表示四边形ABCD的面积S,并求这个矩形面积S的最大值.
如图,在一个半径为r的半圆形铁板中有一个内接矩形ABCD,矩形的边AB在半圆的直径上,顶点C、D在半圆上,O为圆心.令∠BOC=θ,用θ表示四边形ABCD的面积S,并求这个矩形面积S的最大值.分析:根据直角三角形中的三角函数和图形求出矩形的长和宽,再表示出矩形的面积,利用倍角的正弦公式化简,再由正弦函数的最值求出矩形面积的最大值.
解答:解:由图得,BC=rsinθ,AB=2rcosθ,
∴S=AB×BC=2rcosθ×rsinθ=r2sin2θ,
当θ=
时,sin2θ=sin
=1,
∴Smax=r2.
∴S=AB×BC=2rcosθ×rsinθ=r2sin2θ,
当θ=
| π |
| 4 |
| π |
| 2 |
∴Smax=r2.
点评:本题是实际问题为背景,考查了倍角的正弦公式,以及直角三角形中的三角函数,注重数学在实际中的应用.

练习册系列答案
相关题目
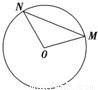
 如图,M是半径为R的圆周上一个定点,在圆周上等可能地任取一点N,连接MN,则弦MN的长度超过
如图,M是半径为R的圆周上一个定点,在圆周上等可能地任取一点N,连接MN,则弦MN的长度超过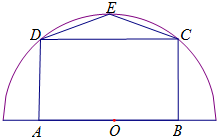 如图,有一块半径为R的半圆形空地,开发商计划征地建一个矩形游泳池ABCD和其附属设施,附属设施占地形状是等腰△CDE,其中O为圆心,A,B在圆的直径上,C,D,E在圆周上.
如图,有一块半径为R的半圆形空地,开发商计划征地建一个矩形游泳池ABCD和其附属设施,附属设施占地形状是等腰△CDE,其中O为圆心,A,B在圆的直径上,C,D,E在圆周上.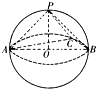 如图所示,已知三棱锥P-ABC的各顶点均在一个半径为R的球面上,球心0在AB上,P0⊥平面ABC,
如图所示,已知三棱锥P-ABC的各顶点均在一个半径为R的球面上,球心0在AB上,P0⊥平面ABC, R的概率是 .
R的概率是 .