题目内容
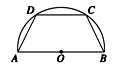
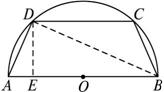
 如图,有一块半径为R的半圆形空地,开发商计划征地建一个矩形游泳池ABCD和其附属设施,附属设施占地形状是等腰△CDE,其中O为圆心,A,B在圆的直径上,C,D,E在圆周上.
如图,有一块半径为R的半圆形空地,开发商计划征地建一个矩形游泳池ABCD和其附属设施,附属设施占地形状是等腰△CDE,其中O为圆心,A,B在圆的直径上,C,D,E在圆周上.(1)设∠BOC=θ,征地面积记为f(θ),求f(θ)的表达式;
(2)当θ为何值时,征地面积最大?
分析:(1)利用f(θ)=2S梯形OBCE,可求f(θ)的表达式;
(2)求导数,确定函数的单调性,即可求得最值.
(2)求导数,确定函数的单调性,即可求得最值.
解答: 解:(1)连接OE,OC,可得OE=R,OB=Rcosθ,BC=Rsinθ,θ∈(0,
解:(1)连接OE,OC,可得OE=R,OB=Rcosθ,BC=Rsinθ,θ∈(0,
)
∴f(θ)=2S梯形OBCE=R2(sinθcosθ+cosθ);
(2)求导数可得f′(θ)=-R2(2sinθ-1)(sinθ+1)
令f′(θ)=0,则sinθ=
∵θ∈(0,
)
∴θ∈(0,
)时,f′(θ)>0,θ∈(
,
)时,f′(θ)<0,
∴θ=
时,f(θ)取得最大,即θ=
时,征地面积最大.
 解:(1)连接OE,OC,可得OE=R,OB=Rcosθ,BC=Rsinθ,θ∈(0,
解:(1)连接OE,OC,可得OE=R,OB=Rcosθ,BC=Rsinθ,θ∈(0,| π |
| 2 |
∴f(θ)=2S梯形OBCE=R2(sinθcosθ+cosθ);
(2)求导数可得f′(θ)=-R2(2sinθ-1)(sinθ+1)
令f′(θ)=0,则sinθ=
| 1 |
| 2 |
∵θ∈(0,
| π |
| 2 |
∴θ∈(0,
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
∴θ=
| π |
| 6 |
| π |
| 6 |
点评:本题考查函数模型的构建,考查导数知识的运用,正确建立函数模型是关键.

练习册系列答案
相关题目
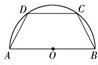 如右图所示,有一块半径为R的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,且上底CD的端点在圆周上,写出梯形周长y关于腰长x的函数关系式,并求出它的定义域.
如右图所示,有一块半径为R的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,且上底CD的端点在圆周上,写出梯形周长y关于腰长x的函数关系式,并求出它的定义域.