题目内容
在R上定义运算⊕:x?y=x(1-y)若对任意x>2,不等式(x-a)?x≤a+2都成立,则实数a的取值范围是( )
分析:由x?y=x(1-y),把(x-a)?x≤a+2转化为(x-a)(1-x)≤a+2,由任意x>2,不等式(x-a)?x≤a+2都成立,知a≤
.令f(x)=
,x>2,则a≤[f(x)]min,x<2.由此能求出结果.
| x2-x+2 |
| x-2 |
| x2-x+2 |
| x-2 |
解答:解:∵x?y=x(1-y),
∴(x-a)?x≤a+2转化为(x-a)(1-x)≤a+2,
∴-x2+x+ax-a≤a+2,
a(x-2)≤x2-x+2,
∵任意x>2,不等式(x-a)?x≤a+2都成立,
∴a≤
.
令f(x)=
,x>2,
则a≤[f(x)]min,x<2
而f(x)=
=
=(x-2)+
+3
≥2
+3=7,
当且仅当x=4时,取最小值.
∴a≤7.
故选C.
∴(x-a)?x≤a+2转化为(x-a)(1-x)≤a+2,
∴-x2+x+ax-a≤a+2,
a(x-2)≤x2-x+2,
∵任意x>2,不等式(x-a)?x≤a+2都成立,
∴a≤
| x2-x+2 |
| x-2 |
令f(x)=
| x2-x+2 |
| x-2 |
则a≤[f(x)]min,x<2
而f(x)=
| x2-x+2 |
| x-2 |
| (x-2)2+3(x-2)+4 |
| x-2 |
=(x-2)+
| 4 |
| x-2 |
≥2
(x-2)•
|
当且仅当x=4时,取最小值.
∴a≤7.
故选C.
点评:本题考查了在新定义下对函数恒成立问题的应用.关于新定义型的题,关键是理解定义,并会用定义来解题.

练习册系列答案
相关题目
 :x
:x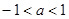 B.0<
B.0< <2 C.
<2 C. D.
D.
 :x
:x B.
B. C.
C. D.
D.