题目内容
15.已知an=n+2,从无穷数列{an}中抽取部分项a${\;}_{{k}_{1}}$,a${\;}_{{k}_{2}}$,…a${\;}_{{k}_{3}}$,…组成一个等比数列{bn},其中1=k1<k2<k3<…<kn<kn+1<…,(n∈N*),kn∈N*,记这个等比数列的公比为q.(1)求证:q∈N*,q≥2;
(2)求证:$\frac{{q}^{n}-1}{q-1}$(n∈N*)是正整数;
(3)设数列{an}的前n项的和为Sn,若存在n∈N*,使Sn≥qn成立,求q的所有可能取值,并证明你的结论.
分析 (1)运用等差数列和等比数列的通项,即可得证;
(2)由(1)的结论和公式$\frac{{q}^{n}-1}{q-1}$=qn-1+qn-2+…+q+1,即可得证;
(3)由(1)的结论,列举q=2,3,4,…,再由二项式定理即可得到结论.
解答 (1)证明:由于an=n+2为整数,
等比数列{bn}中各项均为整数,
即有公比q为正整数,又a${\;}_{{k}_{1}}$=a1=3,
a${\;}_{{k}_{2}}$=k2+2=3q≥2+2,
即q≥$\frac{4}{3}$,由q为整数,
则q≥2;
(2)证明:由bn=b1qn-1=3qn-1,
由(1)q为正整数,
由$\frac{{q}^{n}-1}{q-1}$=qn-1+qn-2+…+q+1,
qn-1,qn-2,…,q均为正整数,
则$\frac{{q}^{n}-1}{q-1}$(n∈N*)是正整数;
(3)解:Sn=$\frac{n(n+5)}{2}$,
若存在n∈N*,使Sn≥qn成立,
即有$\frac{n(n+5)}{2}$≥qn,(q∈N*,q≥2),
当q=2时,n=1,有3>2成立;
当q=3时,n=1,有3=3成立;
当q≥4时,qn>4n,
由2•4n-(n2+5n)=22n+1-(n2+5n)
>1+(2n+1)+$\frac{1}{2}$•2n•(2n+1)-n2+5n
=n2-2n+2>0,
即有4n>$\frac{1}{2}$(n2+5n),
则有$\frac{n(n+5)}{2}$<qn,
综上可得q的取值为2,3.
点评 本题考查等差数列和等比数列的通项和求和公式的运用,同时考查不等式的解法,属于中档题.

练习册系列答案
相关题目
5.若命题p:?x∈R,x>lnx-2,命题q:?x∈R,2x>1,那么( )
| A. | 命题“p或q”为假 | B. | 命题“p且q“为真 | ||
| C. | 命题,“¬p或q”为假 | D. | 命题“p且¬q“为假 |
13.在正方体ABCD-A1B1C1D1中,截面BC1D内的动点P到平面ABCD的距离到顶点C1的距离相等,则动点P的轨迹的离心率为( )
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | 1 | D. | $\frac{\sqrt{3}}{3}$ |
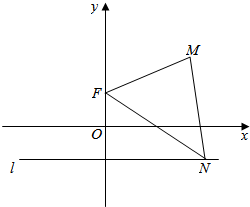 如图,已知点F(0,p),直线l:y=-p(其中p为常数,且p>0),M为平面内的动点,过M作l的垂线,垂足为N,且$\overrightarrow{NM}•\overrightarrow{NF}$=$\overrightarrow{FM}•\overrightarrow{FN}$.
如图,已知点F(0,p),直线l:y=-p(其中p为常数,且p>0),M为平面内的动点,过M作l的垂线,垂足为N,且$\overrightarrow{NM}•\overrightarrow{NF}$=$\overrightarrow{FM}•\overrightarrow{FN}$.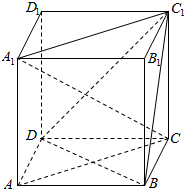 如图,在边长为1的正方体ABCD-A1B1C1D1中,求证:
如图,在边长为1的正方体ABCD-A1B1C1D1中,求证: