题目内容
13.在正方体ABCD-A1B1C1D1中,截面BC1D内的动点P到平面ABCD的距离到顶点C1的距离相等,则动点P的轨迹的离心率为( )| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | 1 | D. | $\frac{\sqrt{3}}{3}$ |
分析 求出P所在平面与底面所成二面角的余弦函数值,转化P到底面的距离为到BD的距离,然后求解离心率.
解答 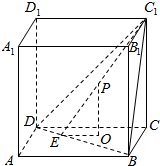 解:由题意可知,截面BC1D与底面ABCD所成的角为:α,设正方体的棱长为1,
解:由题意可知,截面BC1D与底面ABCD所成的角为:α,设正方体的棱长为1,
tanα=$\frac{1}{\frac{\sqrt{2}}{2}}$=$\sqrt{2}$,则cosα=$\frac{\sqrt{3}}{3}$,sinα=$\frac{\sqrt{6}}{3}$,
截面BC1D内的动点P到平面ABCD的距离到顶点C1的距离相等,
设距离为m,则PE=$\frac{\sqrt{6}m}{2}$,
所求曲线的离心率为:$\frac{PC}{PE}$=$\frac{m}{\frac{\sqrt{6}m}{2}}$=$\frac{\sqrt{6}}{3}$.
故选:A.
点评 本题考查二面角的平面角的求法.解析几何与立体几何的综合题目,考查空间想象能力,转化思想的应用,难度比较大.

练习册系列答案
相关题目
3.已知函数f(x)=|x|-1,若关于x的方程f2(x)+(2m-1)f(x)+4-2m=0有四个不同的实数解,则实数m的取值范围是( )
| A. | m<-2 | B. | m<-2.5 | C. | m<1.5 | D. | m>1.5 |
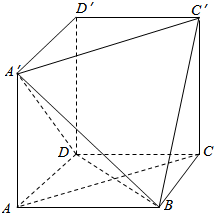 在长方体ABCD-A′B′C′D′中,AB=BC=2,过A′,C′,B三点的平面截去长方体的一个角后,得到ABCD-A′C′D′,
在长方体ABCD-A′B′C′D′中,AB=BC=2,过A′,C′,B三点的平面截去长方体的一个角后,得到ABCD-A′C′D′,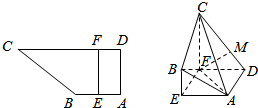 如图所示,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=2,点E在边AB上,点F在边CD上,且EF∥AD,沿EF将面EBCF折起,使得CF⊥AE.
如图所示,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=$\frac{1}{2}$CD=2,点E在边AB上,点F在边CD上,且EF∥AD,沿EF将面EBCF折起,使得CF⊥AE.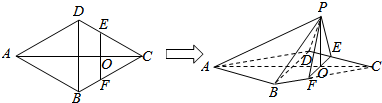
 如图,正方体ABCD-A1B1C1D1中,E是棱B1C1的中点,动点P为正方体各面上的任一点.
如图,正方体ABCD-A1B1C1D1中,E是棱B1C1的中点,动点P为正方体各面上的任一点.