题目内容
19.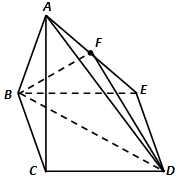 如图等边三角形ABC所在平面与菱形BCDE所在平面互相垂直,F为AE中点,AB=2,∠CBE=60°.
如图等边三角形ABC所在平面与菱形BCDE所在平面互相垂直,F为AE中点,AB=2,∠CBE=60°.(1)求证:AC∥平面BDF;
(2)求点C到平面ABE的距离.
分析 (1)连接EC,EC∩BD=O,连接OF,由线线平行证明线面平行;
(2)将体积等价转化,求出体积,再求出底面面积,从而求高,得距离.
解答  (1)证明:连接EC,EC∩BD=O,连接OF,
(1)证明:连接EC,EC∩BD=O,连接OF,
∵OF为△CAE的中位线,
∴OF∥AC,
∵OF?平面BDF,AC?平面BDF,
∴AC∥平面BDF;
(2)解:取BC的中点M,连接AM,EM,则AM⊥平面BCDE,
由题意,AM=EM=$\sqrt{3}$,AE=$\sqrt{6}$,
△ABE中,AB=BE=2,AE=$\sqrt{6}$,S△ABE=$\frac{1}{2}×\sqrt{6}×\sqrt{4-\frac{6}{4}}$=$\frac{\sqrt{15}}{2}$,
设点C到平面ABE的距离为h,则$\frac{1}{3}×$$\frac{1}{2}×\frac{\sqrt{15}}{2}h$=$\frac{1}{3}×\frac{1}{2}×2×\sqrt{3}×\sqrt{3}$,
∴h=$\frac{4\sqrt{15}}{5}$,
即点C到平面ABE的距离为$\frac{4\sqrt{15}}{5}$.
点评 本题综合考查了空间中线面的位置关系及距离问题,属于中档题.

练习册系列答案
相关题目
10.已知 A={y|y>1},B={x|lnx≥0},则A∩B=( )
| A. | {x|x≥1} | B. | {x|x>1} | C. | {x|0<x<1} | D. | ∅ |
11.已知向量$\overrightarrow{a}$=(an,2),$\overrightarrow{b}$=(an+1,$\frac{2}{5}$),且a1=1,若数列{an}的前n项和为Sn,且$\overrightarrow{a}$∥$\overrightarrow{b}$,则Sn=( )
| A. | $\frac{5}{4}$[1-($\frac{1}{5}$)n] | B. | $\frac{1}{4}$[1-($\frac{1}{5}$)n] | C. | $\frac{1}{4}$[1-($\frac{1}{5}$)n-1] | D. | $\frac{5}{4}$[1-($\frac{1}{5}$)n-1] |
8.若$C_n^{10}=C_n^8$,则$C_{20}^n$=( )
| A. | 380 | B. | 190 | C. | 18 | D. | 9 |
9.已知角α的终边过点P(-8sin390°,-6m),且$cosα=-\frac{4}{5}$,则m为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | ±$\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
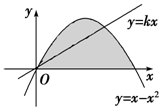 如图直线y=kx及抛物线y=x-x2
如图直线y=kx及抛物线y=x-x2