题目内容
【题目】设函数![]() (
(![]() 为常数),
为常数),![]() 为自然对数的底数.
为自然对数的底数.
(1)当![]() 时,求实数
时,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,求使得
时,求使得![]() 成立的最小正整数
成立的最小正整数![]() .
.
【答案】(1)见解析;(2) 最小正整数![]() 的值为1.
的值为1.
【解析】试题分析:
(1)解不等式![]() ,考虑到
,考虑到![]() 恒成立,可对
恒成立,可对![]() 分类讨论:
分类讨论: ![]() 和
和![]() ;(2)题意就是
;(2)题意就是![]() 恒成立,求
恒成立,求![]() 的最小值正整数,只要求得
的最小值正整数,只要求得![]() 的最小值即可,由于要求得
的最小值即可,由于要求得![]() 的零点,因此还要对此函数进行分析,设
的零点,因此还要对此函数进行分析,设![]() ,利用导数确定它的单调性,从而确定零点
,利用导数确定它的单调性,从而确定零点![]() 的范围,
的范围, ![]() ,再求得最小值
,再求得最小值![]() 的范围,可得结论.
的范围,可得结论.
试题解析:
(1)由![]() 可知
可知![]() ,
,
当![]() 时,
时, ![]() ,由
,由![]() ,解得
,解得![]() ;
;
当![]() 时,
时, ![]() ,由
,由![]() ,解得
,解得![]() 或
或![]() ;
;
当![]() 时,
时, ![]() ,由
,由![]() ,解得
,解得![]() 或
或![]() ;
;
(2)当![]() 时,要使
时,要使![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
令![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,函数
,函数![]() 的
的![]() 上单调递增.
上单调递增.
又因为![]() 时,
时, ![]() ,且
,且![]() ,
,
所以,存在唯一的![]() ,使得
,使得![]() ,
,
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递增.
上单调递增.
所以,当![]() 时,
时, ![]() 取到最小值.
取到最小值.
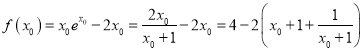 ,
,
因为![]() ,所以
,所以![]() ,
,
从而使得![]() 恒成立的最小正整数
恒成立的最小正整数![]() 的值为1.
的值为1.

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案【题目】某食品店为了了解气温对销售量的影响,随机记录了该店1月份中5天的日销售量![]() (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温![]() (单位:
(单位: ![]() )的数据,如下表:
)的数据,如下表:
x | 2 | 5 | 8 | 9 | 11 |
y | 12 | 10 | 8 | 8 | 7 |
(1)求出![]() 与
与![]() 的回归方程
的回归方程![]() ;
;
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地1月份某天的最低气温为
之间是正相关还是负相关;若该地1月份某天的最低气温为![]() ,请用所求回归方程预测该店当日的销售量;
,请用所求回归方程预测该店当日的销售量;
(3)设该地1月份的日最低气温![]() ~
~![]() ,其中
,其中![]() 近似为样本平均数
近似为样本平均数![]() ,
, ![]() 近似为样本方差
近似为样本方差![]() ,求
,求![]() .
.
附:①回归方程![]() 中,
中, 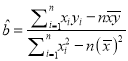 ,
, ![]() .
.
②![]() ,
, ![]() ,若
,若![]() ~
~![]() ,则
,则![]() ,
, ![]() .
.
【题目】在“新零售”模式的背景下,某大型零售公司咪推广线下分店,计划在![]() 市的
市的![]() 区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记
区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记![]() 表示在各区开设分店的个数,
表示在各区开设分店的个数, ![]() 表示这个
表示这个![]() 个分店的年收入之和.
个分店的年收入之和.
| 2 | 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 | 6 |
(1)该公司已经过初步判断,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)假设该公司在![]() 区获得的总年利润
区获得的总年利润![]() (单位:百万元)与
(单位:百万元)与![]() 之间的关系为
之间的关系为![]() ,请结合(1)中的线性回归方程,估算该公司应在
,请结合(1)中的线性回归方程,估算该公司应在![]() 区开设多少个分时,才能使
区开设多少个分时,才能使![]() 区平均每个分店的年利润最大?
区平均每个分店的年利润最大?
(参考公式: ![]() ,其中
,其中 )
)