题目内容

命题“存在x∈R，2x≤0”的否定是（ ）
A．不存在x∈R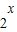，＞0
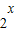B．存在x∈R，≥0
C．对任意的x∈R，2x≤0
D．对任意的x∈R，2x＞0
【答案】分析：根据命题“存在x∈R，≤0”是特称命题，其否定为全称命题，将“存在”改为“任意的”，将“≤”改为“＞”即可得到答案．
解答：解：∵命题“存在x∈R，≤0”是特称命题
∴否定命题为：对任意的x∈R，2x＞0．
故选D．
点评：本题主要考查特称命题与全称命题的转化问题．
练习册系列答案
相关题目
以下正确命题的为
②③④
②③④

①命题“存在x∈R，x2-x-2≥0”的否定是：“不存在x∈R，x2-x-2＜0”；
②函数f(x)=x
1
3
-(
1
2
)x的零点在区间(
1
3
，
1
2
)内；
③在极坐标系中，极点到直线l：ρsin(θ+
π
4
)=
2
的距离是
2
．
④函数f（x）=e-x-ex的图象的切线的斜率的最大值是-2；
⑤线性回归直线
y
=
b
x+
a
恒过样本中心(
.
x
，
.
y
)，且至少过一个样本点．
下列四种说法中，
①命题“存在x∈R，x2-x＞0”的否定是“对于任意x∈R，x2-x＜0”；
②；命题“p且q为真”是“p或q为真”的必要不充分条件；
③已知幂函数f（x）=xα的图象经过点（2，
2
2
），则f（4）的值等于
1
2

④某路公共汽车每7分钟发车一次，某位乘客到乘车点的时刻是随机的，则他候车时间超过3分钟的概率是
4
7
．
说法正确的序号是
③④
③④
．
（2012•青岛二模）以下正确命题的个数为（　　）
①命题“存在x∈R，x2-x-2≥0”的否定是：“不存在x∈R，x2-x-2＜0”；
②函数f(x)=x
1
3
-(
1
2
)x的零点在区间(
1
3
，
1
2
)内； 
③函数f（x）=e-x-ex的图象的切线的斜率的最大值是-2；
④线性回归直线
y
=
b
x+
a
恒过样本中心(
.
x
，
.
y
)，且至少过一个样本点．
有以下命题：
（1）命题“存在x∈R，使x2-x-2≥0”的否定是：“对任意的x∈R，都有x2-x-2＜0”；
（2）已知随机变量ξ服从正态分布N（1，?2），P（ξ≤4）=0.79，则P（ξ≤-2）=0.21；
（3）函数f(x)=x
1
3
-(
1
2
)x的零点在区间(
1
3
，
1
2
)内．
其中正确的命题的个数为（　　）
若命题“存在x∈R，2x2-3ax+9＜0”为假命题，则实数a的取值范围是（　　）
A、[-2
2
，2
2
]
B、[-2，2]
C、[-
2
，
2
]
D、（-2
2
，2
2
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网