题目内容
以下正确命题的为
①命题“存在x∈R,x2-x-2≥0”的否定是:“不存在x∈R,x2-x-2<0”;
②函数f(x)=x
-(
)x的零点在区间(
,
)内;
③在极坐标系中,极点到直线l:ρsin(θ+
)=
的距离是
.
④函数f(x)=e-x-ex的图象的切线的斜率的最大值是-2;
⑤线性回归直线
=
x+
恒过样本中心(
,
),且至少过一个样本点.
②③④
②③④
①命题“存在x∈R,x2-x-2≥0”的否定是:“不存在x∈R,x2-x-2<0”;
②函数f(x)=x
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
③在极坐标系中,极点到直线l:ρsin(θ+
| π |
| 4 |
| 2 |
| 2 |
④函数f(x)=e-x-ex的图象的切线的斜率的最大值是-2;
⑤线性回归直线
 |
| y |
 |
| b |
 |
| a |
. |
| x |
. |
| y |
分析:由含有量词的命题的否定规则,得到①不正确;根据函数零点存在性定理,可得②是真命题;将直线l的极坐标方程化成普通方程,结合点到直线的距离公式加以验证,可得③是真命题;根据导数的运算法则与导数的几何意义,结合基本不等式求最值,可得④是真命题;根据线性回归的概念与性质,可得⑤不正确.由此可得本题的答案.
解答:解:对于①,命题的否定为“任意的x∈R,x2-x-2<0”,所以①不正确;
对于②,因为f(x)=x
-(
)x,满足f(
)=(
)
-(
)^
<0,且f(
)=(
)
-(
)^
>0,
所以函数的零点在区间(
,
),所以②是真命题;
对于③,将极坐标方程化成普通方程,得x+y-2=0,
利用点到直线的距离公式,得极点(0,0)到直线的距离为
d=
=
,故③是真命题;
对于④,函数f(x)=e-x-ex的导数为f′(x)=-e-x-ex=-(ex+
)≤-2,
当且仅当ex=
,即ex=1,x=0时取等号,所以切线的斜率的最大值是-2,得④是真命题;
对于⑤,线性回归直线
=
x+
恒过样本中心(
,
),但不一定过样本点,可得⑤不正确,
综上所述,得其中正确命题为②③④.
故答案为:②③④
对于②,因为f(x)=x
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
所以函数的零点在区间(
| 1 |
| 3 |
| 1 |
| 2 |
对于③,将极坐标方程化成普通方程,得x+y-2=0,
利用点到直线的距离公式,得极点(0,0)到直线的距离为
d=
| |0+0-2| | ||
|
| 2 |
对于④,函数f(x)=e-x-ex的导数为f′(x)=-e-x-ex=-(ex+
| 1 |
| ex |
当且仅当ex=
| 1 |
| ex |
对于⑤,线性回归直线
 |
| y |
 |
| b |
 |
| a |
. |
| x |
. |
| y |
综上所述,得其中正确命题为②③④.
故答案为:②③④
点评:本题给出几个关于函数的零点、函数图象的切线和直线的极坐标方程的几个命题,求其中的真命题.着重考查了含有量词的命题的否定、函数零点存在性定理、导数的运算法则与几何意义和基本不等式求最值等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
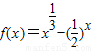 的零点在区间
的零点在区间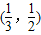 内;
内;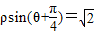 的距离是
的距离是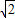 .
.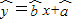 恒过样本中心
恒过样本中心 ,且至少过一个样本点.
,且至少过一个样本点.