题目内容
3.已知函数$f(x)=\left\{\begin{array}{l}{x^2},x≤1\\{2^x},x>1\end{array}\right.$,则f(log23)=3.分析 利用分段函数以及对数运算法则化简求解即可.
解答 解:函数$f(x)=\left\{\begin{array}{l}{x^2},x≤1\\{2^x},x>1\end{array}\right.$,∵log23>log22=1,∴$f({{{log}_2}3})={2^{{{log}_2}3}}=3$.
故答案为:3.
点评 本题考查分段函数的应用,函数值的求法,对数运算法则的应用,考查计算能力.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
18.化简$\sqrt{9{x^2}-6x+1}-{({\sqrt{3x-5}})^2}$,结果是( )
| A. | 6x-6 | B. | -6x+6 | C. | -4 | D. | 4 |
16.如果x,y为实数,且x2-x+(y-1)2=0,则x的取值范围为( )
| A. | 任意实数 | B. | 负实数 | C. | 0<x≤$\frac{1}{2}$ | D. | 0≤x≤1 |
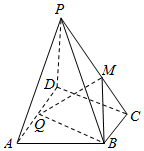 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,PD⊥底面ABCD,∠ADC=90°,AD=2BC,Q为AD的中点,M为棱PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,PD⊥底面ABCD,∠ADC=90°,AD=2BC,Q为AD的中点,M为棱PC的中点. 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=30°,PD⊥平面ABCD,AD=2,点E为AB上一点,且$\frac{AE}{AB}$=m,点F为PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠DAB=30°,PD⊥平面ABCD,AD=2,点E为AB上一点,且$\frac{AE}{AB}$=m,点F为PD中点.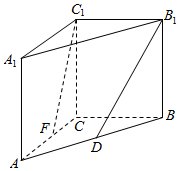 如图所示,在直三棱柱ABC-A1B1C1中,AC=4,BC=4,AA1=4,点D是AB的中点,点E是AC的中点.
如图所示,在直三棱柱ABC-A1B1C1中,AC=4,BC=4,AA1=4,点D是AB的中点,点E是AC的中点.