题目内容
【题目】已知函数![]() ,
, ![]() .
. ![]() 在
在![]() 上有最大值9,最小值4.
上有最大值9,最小值4.
(1)求实数![]() 的值;
的值;
(2)若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若方程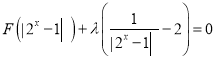 有三个不同的实数根,求实数
有三个不同的实数根,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3)![]()
【解析】试题分析:(1)函数![]() 的对称轴为
的对称轴为![]() ,又
,又![]() ,所以
,所以![]() 在
在![]() 上单调递增,从而得到关于
上单调递增,从而得到关于![]() 的方程组,解之即可;
的方程组,解之即可;
(2)令![]() 不等式
不等式![]() 在
在![]() 上恒成立等价于
上恒成立等价于![]() 在
在![]() 上恒成立,转求
上恒成立,转求![]() 的最小值即可;
的最小值即可;
(3)方程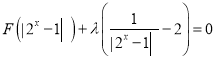 有三个不同的实数根等价于关于
有三个不同的实数根等价于关于![]() 的方程
的方程![]() 有两个不等根,其中一根等于1,一根大于0且小于1,或者一根大于1,一根大于0且小于1,借助二次函数零点的分布情况处理即可.
有两个不等根,其中一根等于1,一根大于0且小于1,或者一根大于1,一根大于0且小于1,借助二次函数零点的分布情况处理即可.
试题解析:
(1)函数![]() 的对称轴为
的对称轴为![]() ,又
,又![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
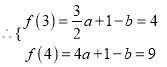 ,解得
,解得![]() .
.
(2)![]() ,
, ![]() ,
,
令![]() ,则
,则![]() ,
,
不等式![]() 可化为
可化为![]() ,
,
所以,问题等价于![]() 在
在![]() 上恒成立,
上恒成立,
因为![]() ,则:
,则: ![]() ,
,
所以: ![]() .
.
(3)令![]() ,图像如下:
,图像如下:
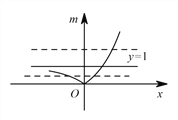
则方程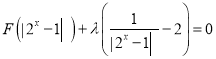 有三个不同的实数根,
有三个不同的实数根,
等价于关于![]() 的方程
的方程![]() 有两个不等根,其中一根等于1,一根大于0且小于1,或者一根大于1,一根大于0且小于1.
有两个不等根,其中一根等于1,一根大于0且小于1,或者一根大于1,一根大于0且小于1.
将![]() 整理成:
整理成: ![]() ,
,
若一根等于1,一根大于0且小于1,将![]() 代入得
代入得![]() ,此时,
,此时, ![]() 只有唯一的根,不符要求,
只有唯一的根,不符要求,
所以,情况为:一根大于1,一根大于0且小于1,
令![]() ,则需满足
,则需满足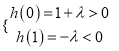 ,解得
,解得![]() .
.
综上所述: ![]() 为所求.
为所求.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目

