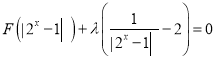题目内容
【题目】如图, ![]() 是平面四边形
是平面四边形![]() 的对角线,
的对角线, ![]() ,
, ![]() ,且
,且![]() .现在沿
.现在沿![]() 所在的直线把
所在的直线把![]() 折起来,使平面
折起来,使平面![]() 平面
平面![]() ,如图.
,如图.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)由平面![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,且
,且![]() ,根据线面垂直的判定定理可得
,根据线面垂直的判定定理可得![]() 平面
平面![]() ;(2)取
;(2)取![]() 的中点
的中点![]() ,连
,连![]() .由
.由![]() ,可得
,可得![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]()
![]()
![]() ,所以
,所以![]() 平面
平面![]() ,因此
,因此![]() 就是点
就是点![]() 到平面
到平面![]() 的距离,在
的距离,在![]() 中,
中, ![]() ,
, ![]() ,所以
,所以![]() .
.
试题解析:(1)证明:因为平面![]()
![]() 平面
平面![]()
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]() .
.
(2)取![]() 的中点
的中点![]() ,连
,连![]() .因为
.因为![]() ,所以
,所以![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]()
![]()
![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() 就是点
就是点![]() 到平面
到平面![]() 的距离,
的距离,
在![]() 中,
中, ![]() ,
, ![]() ,所以
,所以![]() .
.
所以是点![]() 到平面
到平面![]() 的距离是
的距离是![]() .
.
【方法点晴】本题主要考查、线面垂直的判定定理及面面垂直的性质定理,属于中档题. 解答空间几何体中垂直关系时,一般要根据已知条件把空间中的线线、线面、面面之间垂直关系进行转化,转化时要正确运用有关的定理,找出足够的条件进行推理;证明直线和平面垂直的常用方法有:(1)利用判定定理;(2)利用判定定理的推论![]() ;(3)利用面面平行的性质
;(3)利用面面平行的性质![]() ;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.
;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
【题目】为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
收入x(万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y(万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
根据上表可得回归直线方程 ![]() ,其中
,其中 ![]() ,
, ![]() =
= ![]() ﹣
﹣ ![]() ,据此估计,该社区一户居民年收入为15万元家庭的年支出为万元.
,据此估计,该社区一户居民年收入为15万元家庭的年支出为万元.