题目内容
已知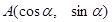 .
.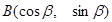 ,其中
,其中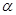 、
、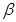 为锐角,且
为锐角,且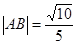 .
.
(1)求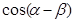 的值;
的值;
(2)若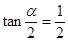 ,求
,求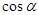 及
及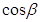 的值.
的值.
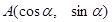 .
.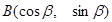 ,其中
,其中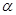 、
、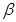 为锐角,且
为锐角,且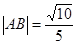 .
.(1)求
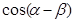 的值;
的值;(2)若
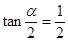 ,求
,求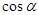 及
及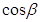 的值.
的值.(1) ;(2)
;(2) ,
, .
.
 ;(2)
;(2) ,
, .
.试题分析:(1)要求
 的值,由于
的值,由于 ,因此我们寻找这两个积(或积的和),这只能应用唯一的已知条件
,因此我们寻找这两个积(或积的和),这只能应用唯一的已知条件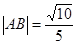 ,由两点间距离公式可得;(2)已知
,由两点间距离公式可得;(2)已知 ,要求
,要求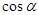 ,可直接利用公式
,可直接利用公式 ,而要求
,而要求 ,要注意灵活应用两角和与差的正弦与余弦公式,我们要把
,要注意灵活应用两角和与差的正弦与余弦公式,我们要把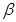 看作为
看作为 ,因此有
,因此有 ,从而只要求出
,从而只要求出 和
和 ,在求解过程中,
,在求解过程中, 的值是确定的,但
的值是确定的,但 的值是一确定的(有两解,至少在开始求解时是这样的),只是在求
的值是一确定的(有两解,至少在开始求解时是这样的),只是在求 时,要舍去不符合题意的结论.
时,要舍去不符合题意的结论.试题解析:(1)由
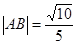 ,得
,得 ,
,得
 ,得
,得 . 4分
. 4分(2)

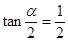 ,
,
 . 6分
. 6分
 ,
, 10分
10分当
 时,
时, .
.当
 时,
时, .
.
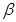 为锐角,
为锐角,
 14分
14分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ;
; ;
; ;
; ;
; .
. 的最大值与最小值.
的最大值与最小值. ).
). 的最大值,并写出
的最大值,并写出 ,b+c=2,求实数a的最小值。
,b+c=2,求实数a的最小值。 中,
中, 分别为角
分别为角 的对边,且
的对边,且 .
. 的最大值.
的最大值. .
. 的单调递增区间;
的单调递增区间; ,求
,求 的值
的值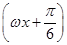 (其中ω>0,x∈R)的最小正周期为10π.
(其中ω>0,x∈R)的最小正周期为10π.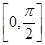 ,f
,f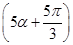 =-
=-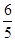 ,f
,f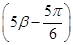 =
=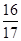 ,求cos(α+β)的值.
,求cos(α+β)的值. tan10°).
tan10°).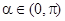 ,且
,且 ,则
,则 的值为( )
的值为( )
