题目内容

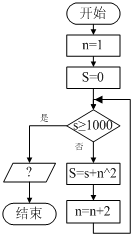求满足12+32+52+…+n2≥1000的最小正整数n的程序框图如图所示，则？处应填入：输出


  1. A.
    n-2
  2. B.
    n
  3. C.
    n-4
  4. D.
    n+2
A
分析：先假设最大正整数n使12+22+32+…+n2＜1000成立，然后利用伪代码进行推理出最后n的值，从而得到我们需要输出的结果．
解答：假设最大正整数n使12+22+32+…+n2＜1000成立
此时的n满足S＜1000，则语句S=S+n2，n=n+1继续运行
此时n=n+2，属于图中输出语句①处应填入n-2
答案为n-2．
故选A．
点评：本题主要考查了当型循环语句，以及伪代码，算法在近两年高考中每年都以小题的形式出现，基本上是低起点题．
练习册系列答案
相关题目
已知平面向量
a
=(
3
，-1)，
b
=(
1
2
，
3
2
)
（1）证明：
a
⊥
b
；
（2）若存在实数k和t，满足
x
=(t+2)
a
+(t2-t-5)
b
，
y
=-k
a
+4
b
，且
x
⊥
y
，试求出k关于t的关系式，即k=f（t）；
（3）根据（2）的结论，试求出函数k=f（t）在t∈（-2，2）上的最小值．
已知函数f（x）=ax2+2x+c（a、c∈N*）满足：①f（1）=5；②6＜f（2）＜11．
（1）求a、c的值；
（2）若对任意的实数x∈[
1
2
，
3
2
]，都有f（x）-2mx≤1成立，求实数m的取值范围．
（2011•合肥三模）已知函数fn(x)=
1
3
x3-
1
2
(n+1)x2+x(n∈N*)，数列{an}满足an+1=f'n（an），a1=3．
（1）求a2，a3，a4；
（2）根据猜想数列{an}的通项公式，并证明；
（3）求证：
1
(2a1-5)2
+
1
(2a2-5)2
+…+
1
(2an-5)2
＜
3
2
．
已知函数f（x）对任意x∈R都有f(x)+f(1-x)=
3
2
．
（1）求f(
1
2
)的值；
（2）若数列{an}满足an=f(0)+f(
1
n
)+f(
2
n
)+…+f(
n-1
n
)+f(
n
n
)  (n∈{N，求数列{an}的通项公式；
（3）设bn=
2
4an-5
 (n∈{N，求数列{Cn}的前n项和Tn．
已知平面向量
a
=（
3
，-1），
b
=（
1
2
，
3
2
）．
（1）若存在实数k和t，满足
x
=（t-2）
a
+（t2-t-5）
b
，
y
=-k
a
+4
b
，且
x
⊥
y
，求出k关于t的关系式k=f（t）；
（2）根据（1）的结论，试求出函数k=f（t）在t∈（-2，2）上的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网