题目内容
已知椭圆的焦点F1(-1,0),F2(1,0),P是椭圆上一点,且|F1F2|是|PF1|,|PF2|等差中项,则椭圆的方程是
- A.
 +
+ =1
=1 - B.
 +
+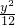 =1
=1 - C.
 +
+ =1
=1 - D.
 +
+ =1
=1
C
分析:根据椭圆和数列的基本性质以及题中已知条件便可求出a和b值,进而求得椭圆方程.
解答:由题意可得:|PF1|+|PF2|=2|F1F2|=4
∴2a=4,2c=2,∴b=3
∴椭圆的方程为 .
.
点评:本题利用椭圆的定义求解椭圆的坐标方程,关键是求出其基本量.
分析:根据椭圆和数列的基本性质以及题中已知条件便可求出a和b值,进而求得椭圆方程.
解答:由题意可得:|PF1|+|PF2|=2|F1F2|=4
∴2a=4,2c=2,∴b=3
∴椭圆的方程为
 .
.点评:本题利用椭圆的定义求解椭圆的坐标方程,关键是求出其基本量.

练习册系列答案
相关题目
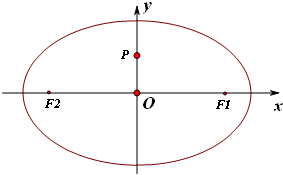 (2012•宝山区一模)已知椭圆的焦点F1(1,0),F2(-1,0),过P(0,
(2012•宝山区一模)已知椭圆的焦点F1(1,0),F2(-1,0),过P(0,