题目内容
已知点A（0，1）是椭圆x2+4y2=4上的一点，P点是椭圆上的动点，则弦AP长度的最大值为（ ）
A、
| ||||
| B、2 | ||||
C、
| ||||
| D、4 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：设点P的坐标为（2cosθ，sinθ），表示出|AP|，利用配方法，即可得出结论．
解答：
解：∵点P在椭圆上，∴设点P的坐标为（2cosθ，sinθ），则|AP|=
=
∴当sinθ=-
时，|AP|最大值为
，
故选：C．
| 4cos2θ+(sinθ-1)2 |
-3(sinθ+
|
∴当sinθ=-
| 1 |
| 3 |
4
| ||
| 3 |
故选：C．
点评：本题考查椭圆方程，考查参数法的运用，考查学生的计算能力，比较基础．
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
命题“存在x0∈R，使2x0≤0”的否定是（ ）
| A、不存在x0∈R，使2x0＞0 |
| B、存在x0∈R，使2x0≥0 |
| C、对任意的x∈R，使2x≤0 |
| D、对任意的x∈R，使2x＞0 |
若
=（2，8），
=（-7，2），则
等于（ ）
| OA |
| OB |
| 1 |
| 3 |
| AB |
| A、（-3，-1） |
| B、（-2，-3） |
| C、（-3，-2） |
| D、（-9，-6） |
已知b＞0，则“ab2＜b”是“ab＜1”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知向量
=（1，x），
=（1，-x），若2
+
与
垂直，则|
|=（ ）
| a |
| b |
| a |
| b |
| b |
| a |
| A、4 | ||
| B、2 | ||
C、
| ||
D、
|
函数f（x）=
的定义域为（ ）
| 1 |
| ln(x+1) |
| A、（-1，0）∪（0，+∞） |
| B、[-1，0）∪（0，+∞） |
| C、[-1，+∞） |
| D、（-1，+∞） |
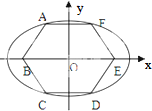如图正六边形ABCDEF中，B、E为椭圆的焦点，A、C、D、F在椭圆上，则椭圆的离心率为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知实数x＞y，且y≠0，则下列结论正确的是（ ）
A、
| ||||
| B、cx＞cy（c∈R） | ||||
| C、x3＞y3 | ||||
D、
|