题目内容
3.已知m,n是两条不重合的直线,α,β是不重合的平面,下面四个命题中正确的是( )| A. | 若m?α,n?β,m⊥n,则α⊥β | B. | 若m∥α,m⊥n,则n⊥α | ||
| C. | 若m⊥α,m⊥β,则α∥β | D. | 若m⊥n,m⊥β,则n∥β |
分析 在A中,α与β相交或平行;在B中,n与α相交、平行或n?α;在C中,由面面平行的判定定理得α∥β;在D中,n∥β或n?β.
解答 解:由m,n是两条不重合的直线,α,β是不重合的平面,知:
在A中:若m?α,n?β,m⊥n,则α与β相交或平行,故A错误;
在B中:若m∥α,m⊥n,则n与α相交、平行或n?α,故B错误;
在C中:若m⊥α,m⊥β,则由面面平行的判定定理得α∥β,故C正确;
在D中:若m⊥n,m⊥β,则n∥β或n?β,故D错误.
故选:C.
点评 本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
15.已知集合M={x|x-2|<1},N={x|y=$\sqrt{4{-2}^{x}}$},则M∩N( )
| A. | (1,2) | B. | (1,2] | C. | (2,3) | D. | [2,3) |
13.已知定义在R上的函数,当x∈[0,2]时,f(x)=8(1-|x-1|),且对任意的实数x∈[2n-2,2n+1-2](n∈N*,且n≥2),都有f(x)=$\frac{1}{2}f({\frac{x}{2}-1})$,若方程f(x)=|logax|有且仅有四个实数解,则实数a的取值范围为( )
| A. | $({\sqrt{2},\sqrt{10}})$ | B. | $[{\sqrt{2},\sqrt{10}}]$ | C. | (2,10) | D. | [2,10] |
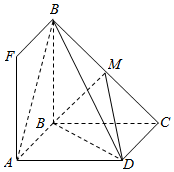 如图,正方形ABCD与正方形ABEF有一条公共边AB,且平面ABCD⊥平面ABEF,M是EC的中点,AB=2.
如图,正方形ABCD与正方形ABEF有一条公共边AB,且平面ABCD⊥平面ABEF,M是EC的中点,AB=2.